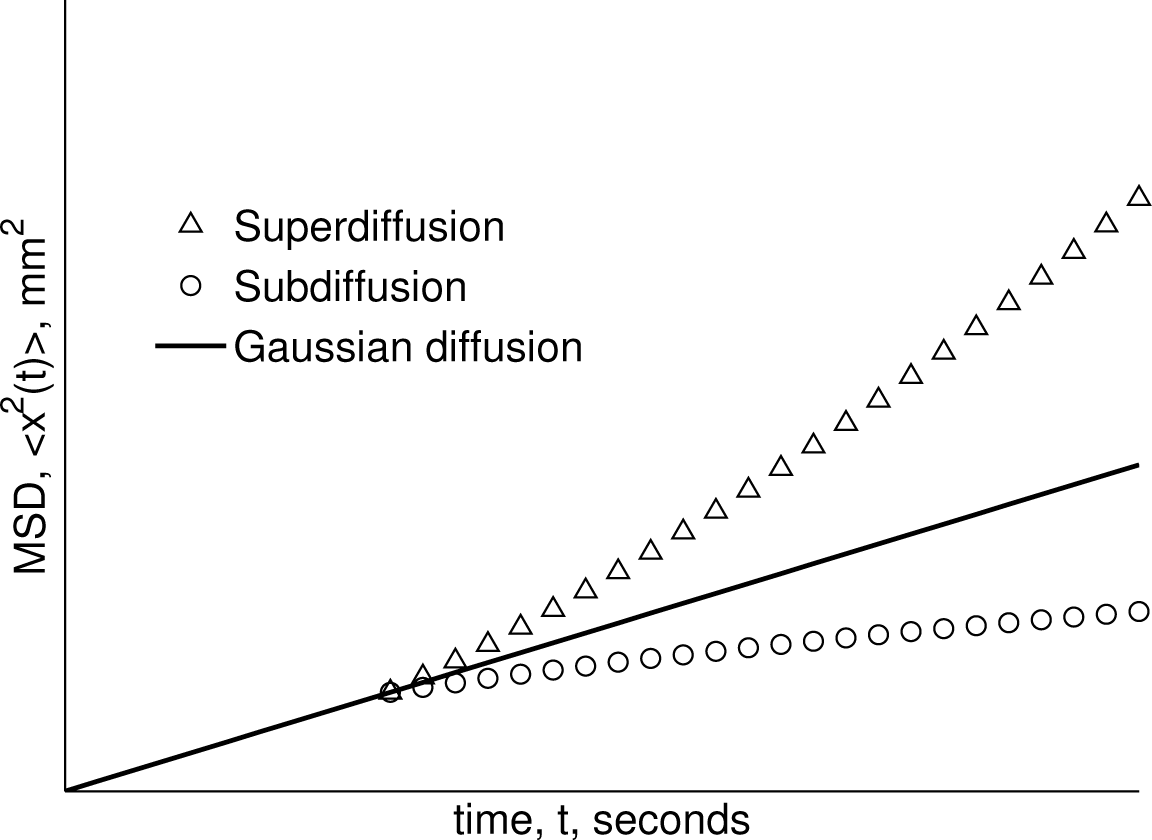
3.1. Diffusion MRI Experiments
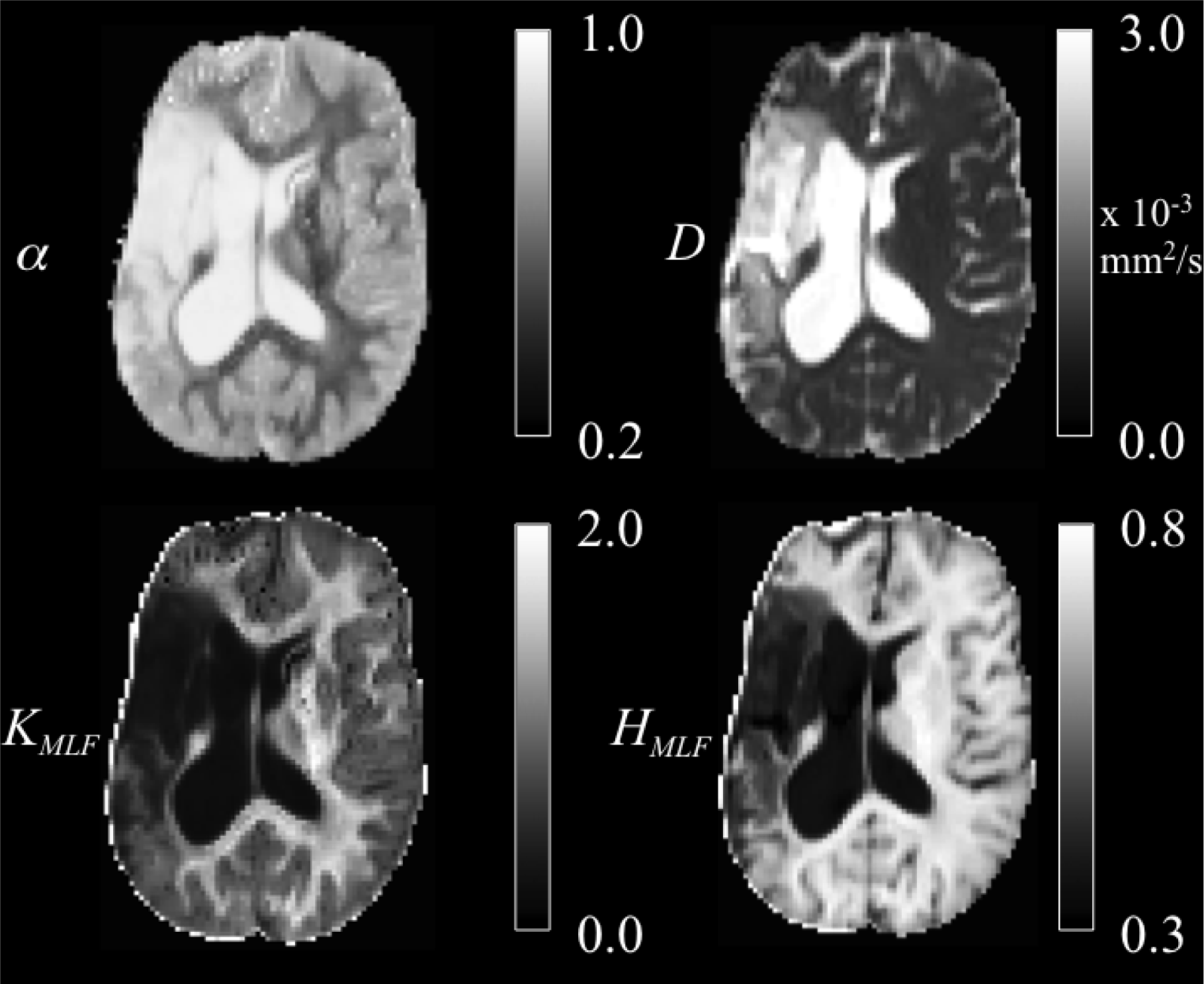
The ischemic tissue (IT), in the right hemisphere of the patient’s brain (left side of the image), has a diffusion coefficient, D, value (∼ 3 × 10−3 mm2/s), which is similar to the typical value found for the cerebral spinal fluid (CSF) of the ventricles. As can be seen in the contralateral hemisphere, prior to the onset of the stroke, the brain slice would have appeared symmetrical with white matter (WM) and gray matter (GM) voxels. However, as these data were acquired ∼ 2 years following onset, the IT microstructure has degenerated (necrosis), such that the bulk diffusion coefficient has increased to an unhindered value. Furthermore, the diffusion in the IT is close to Gaussian as α ∼ 1, indicating a monoexponential behavior, which is also the case for the CSF. The trace values for D in the healthy WM and GM are ∼ 1/3 of the values in the IT and CSF, with the WM possessing an overall slower diffusion than measured in the GM.
As the scale in the
D map in
Figure 4 spans 3 × 10
−3 mm
2/s, the contrast between WM and GM is difficult to discern; however, in the
α map, the WM/GM contrast is clearly visible with the WM demonstrating more subdiffusive behavior compared to the GM. The
KMLF map also has clearly visible GM/WM contrast and appears as a negative image in the
α map, due to the nearly inverse relationship between
KMLF and
α in
Equation (19). The entropy,
HMLF, map provides a stable image in which there is visible and smooth GM/WM contrast, with the IT and CSF exhibiting low values of entropy due to the unhindered Gaussian diffusion dynamics. Interestingly, voxels exhibiting low values of
α, representing highly subdiffusive dynamics, also have relatively high entropy estimations (particularly in the WM) to indicate a diffusion propagator with a heavy-tailed pdf. In correspondence with entropy, there is high kurtosis estimated for the diffusion propagator pdf in regions of low values of
α. However, kurtosis and entropy are not interchangeable measures of the diffusion propagator pdf, evident not only in the images shown in
Figure 4, but also mathematically distinct in the forms of
Equations (19) and
(22). Specifically, in consideration of the CF,
α and
KMLF are measures of the deviation from a monoexponential form with a rate of the diffusion coefficient,
D, whereas entropy considers the entire CF, which includes both the monoexponential component,
D, and the non-Gaussian component,
α, of the diffusion profile. As kurtosis is defined as the normalized fourth moment in
Equation (16), it can be readily seen that the variance, or
D, is canceled out when dividing
Equation (18) by
Equation (13).
Utilizing the moment expansion of the time-fractional form of the MLF in
Equations (13) and
(18) provides a direct link for kurtosis to subdiffusion through the Γ function and
α. As
Equation (9) is an analytic and monotonically decreasing function, the MLF provides the opportunity to more completely sample wavenumber and diffusion time distributions, to more accurately estimate the true kurtosis of the diffusion propagator, which is an advantage compared to other approaches that estimate kurtosis through Taylor expansion of the exponential function [
18].
3.2. Measuring the Mittag–Leffler Function with Spectral Entropy
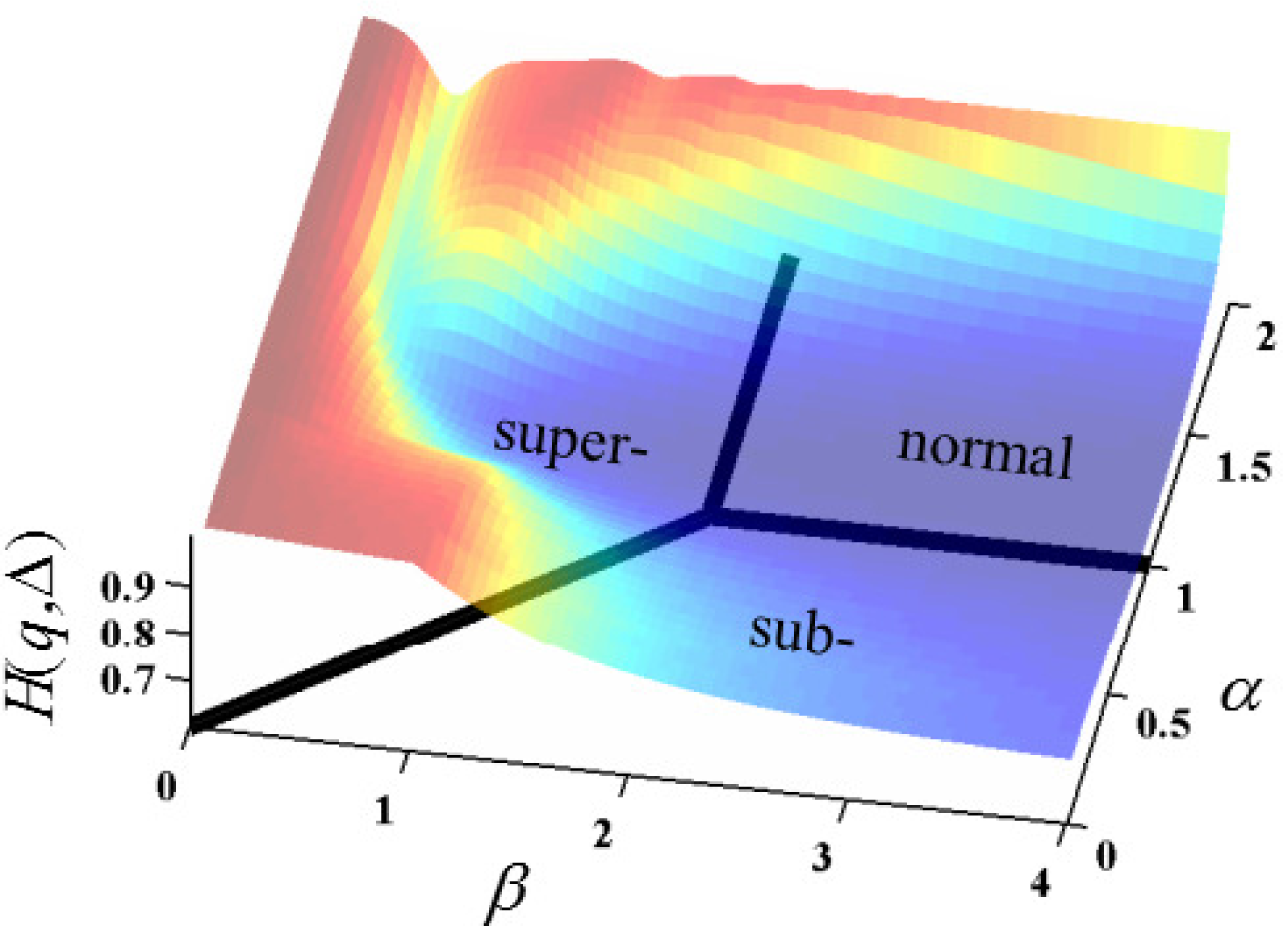
In
Figure 5, the overall shape of the surface resembles plateaus of high entropy at non-integer values of
α and
β with a canyon of low entropy (near
α = 1) that flows in the direction of increasing
β. The Gaussian case (
α = 1 and
β = 2) is at a minimum for permutations of
α ≤ 1 and
β ≤ 2. Of course, the specifics of the cross-sectional shape and entropy values of the surface is subject to change, with values chosen for the values of
D and
t as detailed in the analyses provided by
Figures 6–
9.
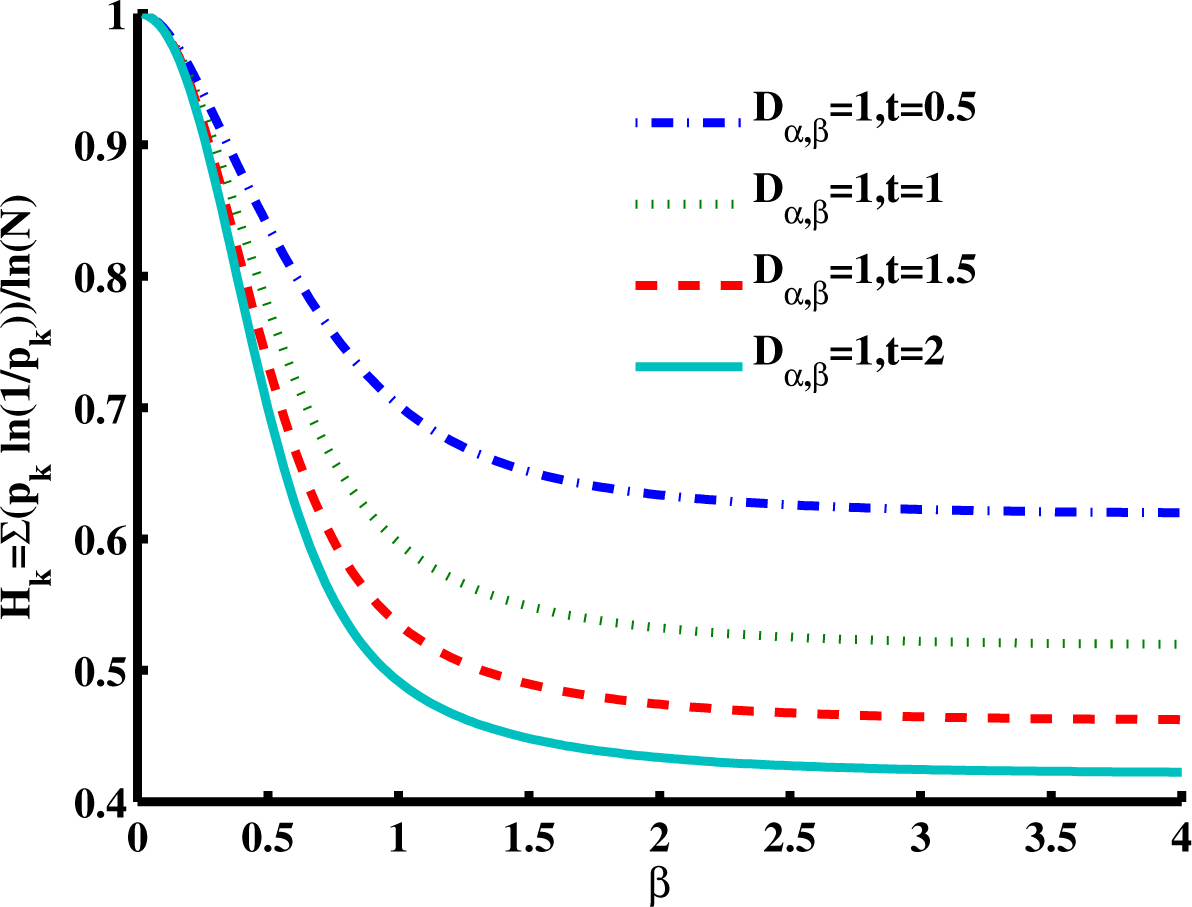
Figure 6 is a slice of the spectral entropy surface (for
α = 1 and four values of time) from the
β = 0 rim out to the distance of
β = 4. Selecting one case of the argument, say
D1,β = 1,
t = 1, and starting at
β = 2, we observe that the entropy increases as
β gets smaller, with an approximately 20% increase in the normalized spectral entropy when
β = 1 (the Cauchy distribution), whereas travel in the direction of increasing
β is mostly flat by this measure of entropy. From the Gaussian location,
β = 2, the entropy appears to converge to a value near 0.5 for increasing
β, while for decreasing
β, the entropy increases in a monotonic manner at short times. The effect of increasing diffusion time (or larger values of the diffusion coefficient) results in a decrease in the magnitude for the normalized entropy values, as demonstrated going from
t = 0.5 to
t = 2. In the phase diagram (
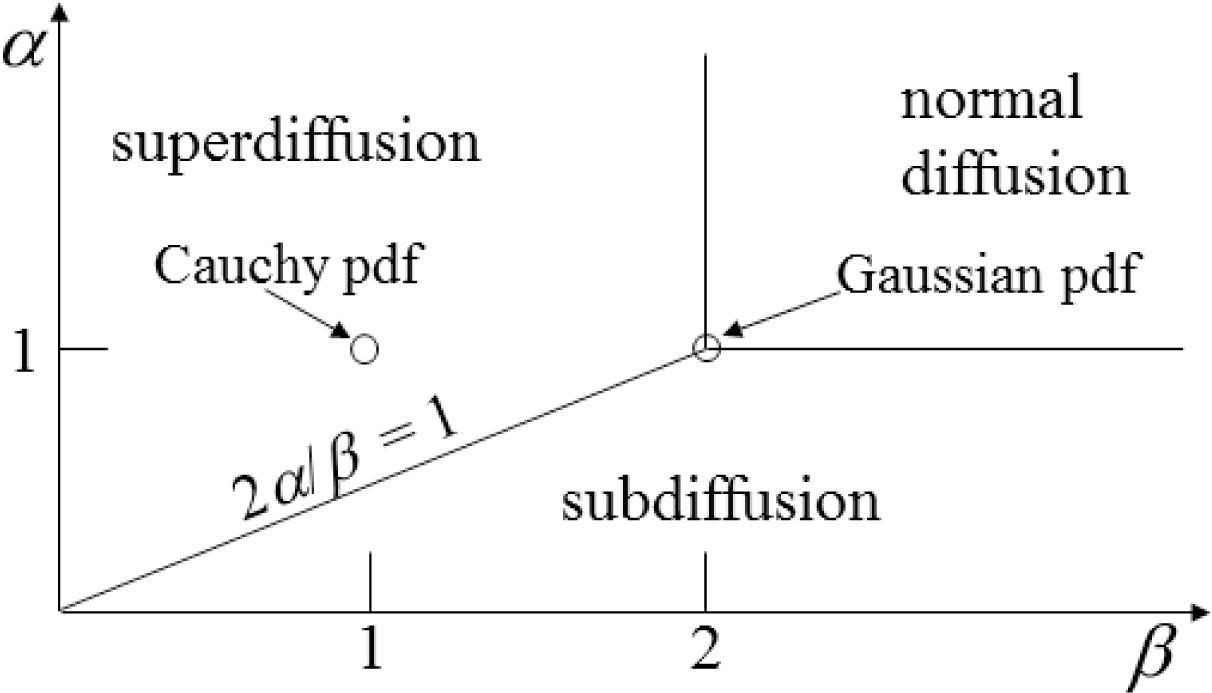
Figure 2:
α = 1 and
β < 2),
Figure 6 evaluates the case of super-diffusion, and it is encouraging that this perspective portrays this regime, which includes the CF of the Cauchy distribution, as one of higher entropy (in comparison with the Gaussian diffusion case).
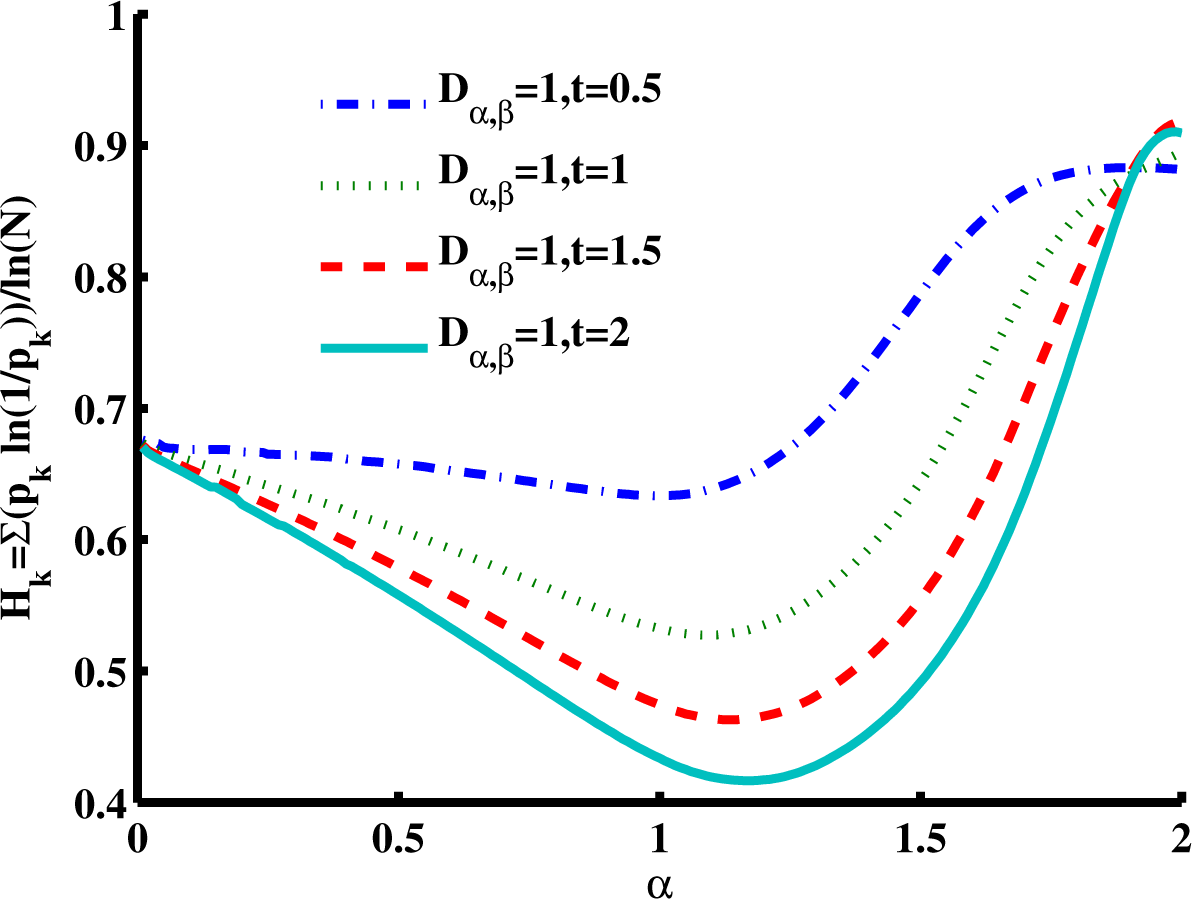
Figure 7 is a slice of the spectral entropy surface (for
β = 2 and four values of time) from the
α = 0 rim out to the distance of
α = 2. Selecting one case of the argument, say
Dα,2 = 1,
t = 1, and starting at
α = 1, we observe the entropy increasing in both directions, overall. Again, the depth of the minimum grows for longer times, but in this cross-sectional view, the location is in the direction of higher values of
α. As is shown in the phase diagram (
Figure 2), when
β = 2, values of
α > 1 are in a region of super-diffusion and values of
α < 1 are in a region of subdiffusion. Furthermore, in
Figure 7, we observe that for a specific value of time (and diffusion coefficient constant), the entropy generally increases (from the Gaussian diffusion case of
α = 1) as the value of
α increases, as well as as it decreases. Thus, both higher and lower values of the order of the fractional derivative
α (relative to
α = 1) give higher entropy values.
In both
Figure 6 and
Figure 7, it is interesting to note that as the product of the diffusion coefficient and the time increases, the spectral entropy decreases. Mathematically, this behavior is consistent with the Fourier- transform duality between the space and the wavenumber (spatial frequency) domains, in which the diffusion coefficient and time,
Dt, change position from the denominator to the numerator of the argument (see
Equation (5) and
Equation (6) for the case of a Gaussian pdf). Thus, as diffusion time increases, in the framework of the space domain, we expect the distribution to widen and the entropy to increase (increasing variance for the Gaussian). Conversely, as the diffusion time increases, in the framework of the spatial frequency domain, we expect the distribution to narrow and the entropy to decrease. From a CTRW physical model perspective, as the diffusion time increases in the spatial domain, we argue that the distribution widens and the entropy increases as a dynamic measure by which the uncertainty in predicting the location of the diffusing particle increases. As such, more information is required to specify the spatial location of the particle as the diffusion time increases. Conversely, as the diffusion time increases in the spatial frequency domain, we argue that the distribution narrows and the entropy decreases as a dynamic measure by which the amount of information to be gained about the diffusion environment decreases. Therefore, as the CTRW process progresses in time, the environment becomes completely explored, and no new information can be captured about the system, albeit at the cost of maximum uncertainty about the particle’s location in space.
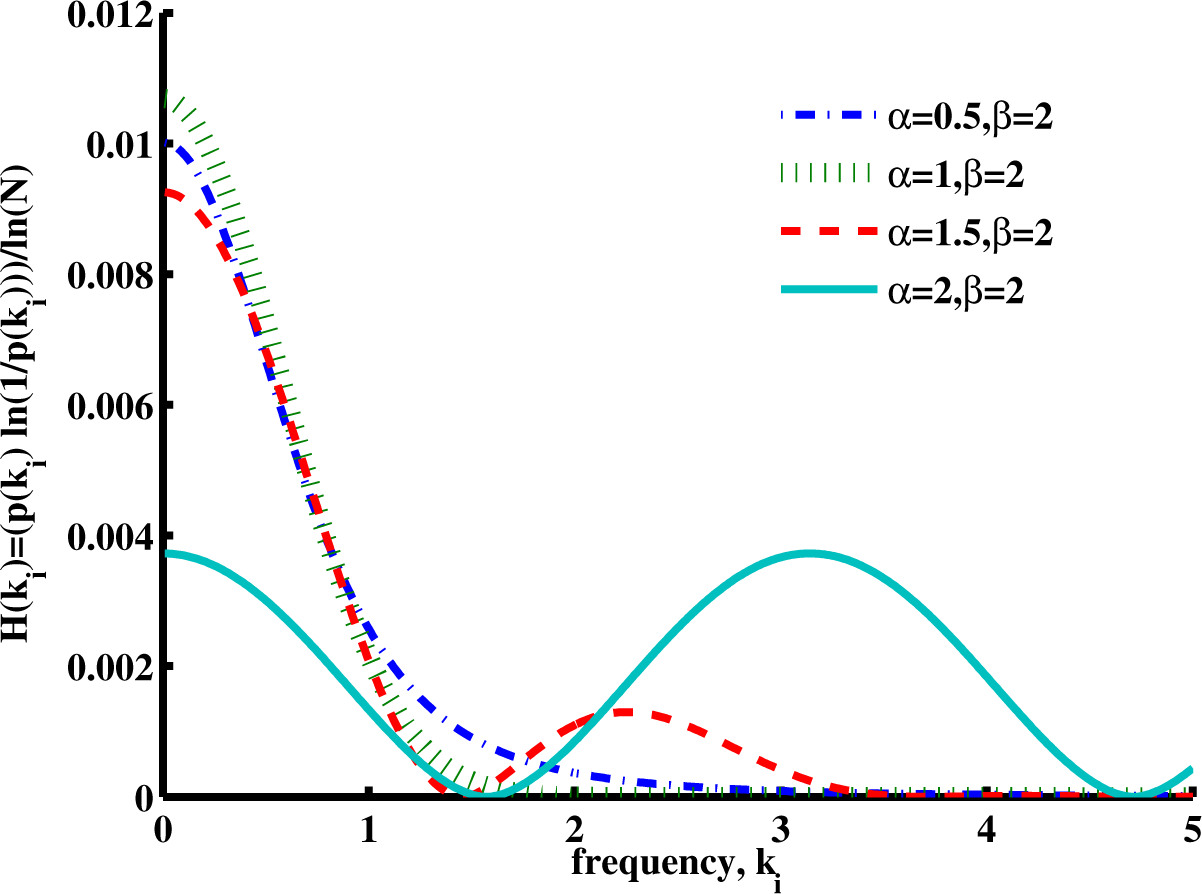
In order to examine further the factors that are summed in
Equation (22), we have plotted (for a fixed diffusion coefficient and time) a single spectral entropy term as a function of the wavenumber for a series of
β values in
Figure 8 (stretched exponential function) and a series of
α values in
Figure 9 (stretched MLF). Here, for
β = 2, the characteristic Gaussian shape is apparent, and as
β decreases into the domain of super-diffusion, the spectrum appears to narrow, but in fact, due to the long power law tail, it actually spreads out, expanding the number and the range of higher wavenumber components. The sum of many of these terms can be interpreted as adding information to the corresponding spatial distribution, increasing its variance and its entropy. Furthermore, in this figure, we note that the Cauchy distribution (
β = 1) has, in comparison with the Gaussian distribution, a wider spectral distribution, with a corresponding increase in spatial complexity and entropy.
The spectral entropy plotted in
Figure 9 has similar features. For
α = 1, the expected Gaussian distribution of spectral entropy is apparent. When
α is reduced to 0.5, the spectra expand (higher uncertainty, higher entropy), and when
α is increase to 1.5 and to 2, an oscillation appears in the spectra due to the behavior of the MLF, which again pushes more wavenumber components into the higher range. Such components would be expected to add uncertainty and entropy to the spatial distribution. In the case of
α = 2, we have a cosine function in the wavenumber, which corresponds to a single, very small spatial feature (a Dirac Delta function) in space.