Inferring a Drive-Response Network from Time Series of Topological Measures in Complex Networks with Transfer Entropy
Abstract
: Topological measures are crucial to describe, classify and understand complex networks. Lots of measures are proposed to characterize specific features of specific networks, but the relationships among these measures remain unclear. Taking into account that pulling networks from different domains together for statistical analysis might provide incorrect conclusions, we conduct our investigation with data observed from the same network in the form of simultaneously measured time series. We synthesize a transfer entropy-based framework to quantify the relationships among topological measures, and then to provide a holistic scenario of these measures by inferring a drive-response network. Techniques from Symbolic Transfer Entropy, Effective Transfer Entropy, and Partial Transfer Entropy are synthesized to deal with challenges such as time series being non-stationary, finite sample effects and indirect effects. We resort to kernel density estimation to assess significance of the results based on surrogate data. The framework is applied to study 20 measures across 2779 records in the Technology Exchange Network, and the results are consistent with some existing knowledge. With the drive-response network, we evaluate the influence of each measure by calculating its strength, and cluster them into three classes, i.e., driving measures, responding measures and standalone measures, according to the network communities.1. Introduction
1.1. Problem Statement
The last decade has witnessed a flourishing progress of network science in many interdisciplinary fields [1–3]. It is proved both theoretical and practically that topological measures are essential to complex network investigations, including representation, characterization, classification and modeling [4–8]. Over the years, scientists have constantly introduced new measures in order to characterize specific features of specific networks [9–13]. Each measure alone is of practical importance and can capture some meaningful properties of the network under study, but when so many measures are put together we will find that they are obviously not “Mutually Exclusive and Collectively Exhaustive”, namely, some measures fully or partly capture the same information provided by others while there are still properties that cannot be captured by any of the existing measures. Having an overwhelming number of measures complicates attempts to determine a definite measure-set that would form the basis for analyzing any network topology [14,15]. With the increasing popularity of network analyses, the question which topological measures offer complementary or redundant information has become more important [13]. Although it might be impossible to develop a “Mutually Exclusive and Collectively Exhaustive” version of measure-set at present, there is no doubt that efforts to reveal the relationships among these measures could give valuable guidance for a more effective selection and utilization of the measures for complex network investigations.
1.2. Related Works
The relationship of topological measures has been a research topic for several years [4,14–28], and there mainly exist two paradigms, i.e., analytical modeling and data-driven modeling. For a few topological measures of model networks, i.e., networks generated with certain algorithm, some analytical interrelationships are found. For example, the clustering coefficient C of generalized random graphs are functions of the first two moments of the degree distribution [16], and for the small world model, the clustering coefficient C could be related to the mean degree and rewiring probability [17]. The relationship between the average path length and its size in a star-shaped network can be derived as: Lstar=2−2/N [18], while for a Barabási-Albert scale-free network, the relationship between them is: L~ln N/ln ln N [19]. The advantage of the analytical modeling is that the resulting relationships are of rigorous mathematical proofs, but this paradigm imposes limitations in that only a small part of the relationships can be derived analytically, and it is not sure whether these conclusions still hold true for real-life networks. If enough is known about the measures and the way in which they interact, a fruitful approach is to construct mechanism models and compare such models to experimental data. If less is known, a data-driven approach is often needed where their interactions are estimated from data [20]. In other words, when the intrinsic mechanism of real-life network is not clear, the situation we will be concerned with here, the data-driven paradigm might be more suitable. Some of the relevant papers following the data-driven paradigm are reviewed as follows.
Jamakovic et al. [14] collected data from 20 real-life networks from technological, social, biological and linguistic systems, and calculated the correlation coefficients between 14 topological measures. It was observed that subsets of measures were highly correlated, and Principal Component Analysis (PCA) showed that only three dimensions were enough to retain most of the original variability in the data, capturing more than 99% of the total data set variance. Li et al. [21] investigated the linear correlation coefficients between nine widely studied topological measures in three classical complex network models, namely, Erdős-Rényi random graphs, Barabási-Albert graphs, and Watts-Strogatz small-world graphs. They drew a similar conclusion, namely that the measure correlation pattern illustrated the strong correlations and interdependences between measures, and argued that the both these three types of networks could be characterized by a small set of three or four measures instead of by the nine measures studied. Costa et al. [4] summarized dozens of topological measures in their review paper and conducted correlations analysis between some of the most traditional measures for Barabási-Albert (BA) network, Erdős-Rényi (ER), and Geographical Networks (GN). They found that particularly high absolute values of correlations had been obtained for the BA model, with low absolute values observed for the ER and GN cases. Further, they found that the correlations obtained for specific network models not necessarily agreed with that obtained when the three models were considered together. Roy et al. [22] studied 11 measures across 32 data sets in biological networks, and created a heat map based on paired measures correlations. They concluded that the correlations were not very strong overall. Filkov et al. [23] also used a heat map and multiple measure correlations to compare networks of various topologies. They correlated 15 measures across 113 real data sets which represented systems from social, technical, and biological domains. They also found that the 15 measures were not coupled strongly. Garcia-Robledo et al. presented an experimental study on the correlation between several topological measures of the Internet. By drawing bar plot of the average correlation for each measure, they recognized the average neighbor connectivity as the most correlated measure; with the correlation heat map, they concluded that distance measures were highly correlated [24]. Bounova and de Weck proposed an overview of network topology measures and a computational approach to analyze graph topology via multiple-metric analysis on graph ensembles, and they found that density-related measures and graph distance-based measures were orthogonal to each other [25].
More recently, Li et al. explored the linear correlation between the centrality measures using numerical simulations in both Erdős-Rényi networks and scale-free networks as well as in real-world networks. Their results indicated that strong linear correlations did exist between centrality measures in both ER and SF networks, and that network size had little influence on the correlations [26]. Sun and Wandelt performed regression analysis in order to detect the functional dependencies among the network measures, and used the coefficient of determination to explain how well the measures depended on each other. They built a graph for the network measures: each measure was a node and a link existed if there was a functional dependency between two measures. By setting a threshold, they got a functional network of the measures with six connected components [27]. Lin and Ban focused on the evolution of the US airline system from a complex network perspective. By plotting scatter diagrams and calculating linear correlations, they found that there was a high correlation between “strength” and “degree”, while “betweenness” did not always keep consistent with “degree” [28].
The abovementioned researches all follow the data-driven paradigm, and provide convincing arguments in favor of using the statistical approach to correlate the measures. The correlations between topological measures strongly depend on the graph under study [14], and results from these studies differ greatly. Some of them argue that most of the measures are strongly correlated and thus can be redundant, while others argue that these correlations are not strong overall. Even the resulting correlation patterns of the same measures in different networks are not consistent. Just as Bounova and de Weck pointed out that pulling networks from different domains together for statistical analysis might provide incorrect conclusions, because there often exists considerable diversity among graphs that share any given topology measures, patterns vary depending on the underlying graph construction model, and many real data sets are not actual statistical ensembles [25].
1.3. Primary Contribution of This Work
To address the issue mentioned above, we resort to two research strategies:
On the one hand, our investigation will be based on data observed from the same network, instead of data pieced together from different networks in several fields. More specially, we will record the trajectories of the measures of the same system, and try to infer their relationships from simultaneously measured time series of these measures.
On the other hand, our investigation will adopt another data-driven method, i.e., transfer entropy. Since our data is in the form of time series, transfer entropy, instead of correlation coefficients or other model-based methods, might be a better choice for our purpose. There are at least two reasons. For one thing, the correlation measure is designed for static data analysis and when applying to time series data, all dynamical properties of the series are discarded [29]. For another, correlations, linear or nonlinear, only indicate the extent to which two variables behave similarly. They cannot establish relationships of influence, since the interactions between the measures are not necessarily symmetric. Neither can they indicate if two measures are similar not because they interact with each other, but because they are both driven by a third [30]. We need a novel tool not only to detect synchronized states, but also to identify drive-response relationships. These issues can be addressed by measures of information transfer. One such measure is Schreiber’s Transfer Entropy [31], which is with minimum of the assumption of the dynamic of the system and the nature of their coupling.
This paper will follow the data-driven paradigm and employ transfer entropy as a quantitative description of interactions among topological measures. Transfer entropy has been proposed to distinguish effectively driving and responding elements and to detect asymmetry in the interaction of subsystems. It is it widely applicable because it is model-free and sensitive to nonlinear signal properties [32]. Thus the transfer entropy is able to measure the influences that one measure can exert over another. On the basis of these pair-wise relationships, we will construct a so-called drive-response network with the measures as its nodes and the pair-wise relationships as its edges. The resulting network will enable us to gain a deeper insight into patterns and implications of relationships among network topological measures. In this paper, we mainly consider the following fundamental questions:
Whether or not there exist drive-response relationships between topological measures? For example, will the network diameter influence the average path length? If that is the case, how to measure the strength of this relationship?
What does the overall picture look like when measures are put together? What is the structure of the measure-set? Can the measures be grouped into different communities?
Are all the measures equally important? If not so, how to identify the pivotal ones?
In order to conduct our investigation, high-quality data is necessary. It is usually difficult to obtain the evolutional record of complex network [33]. Thanks to the advanced information systems in Beijing Technology Market Management Office (or BTMMO, for short), we are able to collect a complete data set which describe the evolution of the Technology Exchange Network day by day. Our proposed method will take the Technology Exchange Network as an empirical application, which allowing us to study several measures across as many as 2779 datasets.
The remainder of this paper is organized as follows: the next section will synthesize a transfer entropy-based framework to infer and analyze the drive-response network. The emphasis is on how to quantify the relationships among time series which are continuous, non-stationary, and of finite sample effect and indirect effect. Section 3 will apply the proposed framework to an empirical investigation on the Technology Exchange Network. Some concluding remarks are made in Section 4.
2. Methodology
2.1. Main Principle
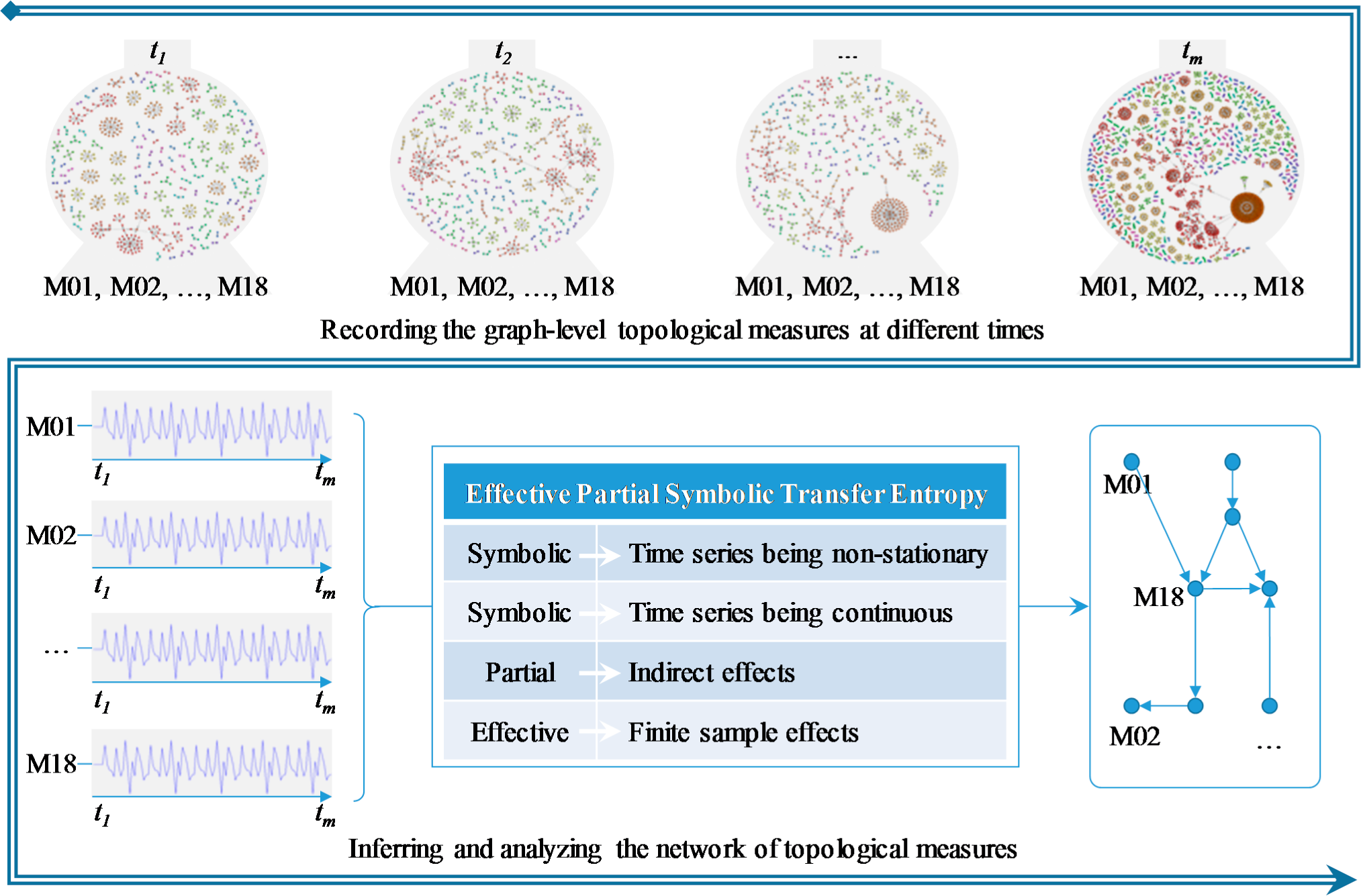
The proposed method is to mine the overall pattern of the relationships among network topological measures from their time series, which is shown in Figure 1.
The relationships here refer in particular to drive-response relationships. A convenient way to represent drive-response relations between two variables is to connect these two with a directed edge, and correspondingly the overall relation pattern can be illustrated in the form of a network. The tool for network inference is the transfer entropy, which is proposed by several researchers for revealing networks from dynamics [34,35].
It is worth noting that what is to be constructed here is the network of measures, which should not be confused with the original network of units. As shown in the upper half of Figure 1, we will trace the original network at successive time points, acquiring time series for each topological measure. And we will quantify the relationships between measures based on these time series with transfer entropy, and then construct a drive-response network which stands for the relation pattern among these topological measures, as shown in the lower half of Figure 1.
The process of inferring the drive-response network is as follows: The network can be presented by a set V of nodes and a set E of edges, connected together as a directed graph denoted G = (V, E). The nodes here are the measures, and the edges are the drive-response couplings between any two measures. In our study, the couplings are detected by transfer entropy. Namely, connectivity is based on the estimation of the influence one measure v exerts on another measure u. If there exists significant coupling, there will be a directed edge from v to u. The resulting network is also a weighted one, with the transfer entropy value as the weight of each edge.
Once the drive-response network is constructed, we may gain in-depth understanding of the relationships among the measures by analyzing the network. For example, we can calculate the prestige of each node to reveal which measures are more influential, and we can cluster the measures into different groups by detecting the communities in the network.
The main steps of the proposed method are as follows:
Step 1: Time Series Observation on Topological Measures. Record the graph-level topological trajectories in form of simultaneously measured time series
Step 2: Drive-response Network Inference. Calculate the transfer entropy between each pair of measures based on their time series, assess the statistical significance and construct the drive-response network.
Step 3: Drive-response Network Analysis. Calculate the prestige of each node and detect community to gain a deep understanding.
The process will be explained step by step in more details in the following section.
2.2. Main Steps
2.2.1. Time Series Observation on Topological Measures
In our study, the data is collected from observation of the same system. We will track the topological measures of an evolving network at successive points in time spaced at uniform time intervals, resulting in sequences of observations on topological measures which are ordered in time. The topological measures to be investigated in our study are discussed as follows.
Topological measures can be divided in two groups, i.e., measures at global network level and measures at local node level [27,36], corresponding to the measurable element. Local topological measures characterize individual network components while global measures describe the whole network [37]. Since the observed object in our study is the network as a whole, only those graph-level measures will be selected. In other words, node-level such as the degree of a certain node will not be taken into account.
Due to the fact that the number of proposed measures is overwhelming and new measures are introduced every day, there is no consensus on a definitive set of measures that provides a “complete” characterization of real-world complex networks [24] and no classifications of these measures are universally accepted. On the basis of several important and influential works such as [4,9,25], we will classify these measures into four categories, i.e., Category I, Distance Relevant Measures; Category II, Centralization Measures; Category III, Connection Measures; Category IV, Entropy and other Complexity Measures. We will select a few measures from each of the four categories and conduct our investigation on these selected measures.
Measures selected from Category I: M01, Average Path Length; M02, Diameter; M03, Eccentricity; M04, Integration; M05, Variation. All of them are based on distance. For example, the average path length is defined as the average number of steps along the shortest paths for all possible pairs of network nodes. Diameter is the greatest distance between any pair of vertices. The eccentricity in the local node level is defined as the greatest distance between v and any other vertex, and eccentricity in the global network level is the sum of all the vertices eccentricities. Graph integration is based on vertex centrality while variation is based on vertex distance deviation.
Measures selected from Category II: M06, Centralization; M07, Degree Centralization; M08, Closeness Centralization; M09, Betweenness Centralization; M10, Eigenvector Centralization. In local node level, centrality is to quantify the importance of a node. Historically first and conceptually simplest is degree centrality, which is defined as the number of links incident upon a node. The closeness of a node is defined as the inverse of the farness, which is the sum of its distances to all other nodes. Betweenness centrality quantifies the number of times a node acts as a bridge along the shortest path between two other nodes. The corresponding concept of centrality at the global network level is centralization. In our study, we will employ Freeman’s formula [38] to calculate graph-level centralization scores based on node-level centrality.
Measures selected from Category III: M11, Vertex Connectivity; M12, Edge Connectivity; M13, Connectedness; M14, Global Clustering Coefficient; M15, Assortativity Coefficient. These measures refer to connection. For example, the vertex connectivity is defined as the minimum number of nodes whose deletion from a network disconnects it. Similarly, the edge connectivity is defined as the minimum number of edges whose deletion from a network disconnects it. Connectedness is defined as the ratio of the number of edges and the number of possible edges. It measures how close the network is to complete. Global Clustering coefficient is to quantify the overall probability for the network to have adjacent nodes interconnected. It is also called second order extended connectivity, which can be calculated by counting the edges between the second neighbors of vertex, and again comparing that count to the number of edges in the complete graph that could be formed by all second neighbors. Assortativity is defined as the Pearson correlation coefficient of the degrees at both ends of the edges. This measure reveals whether highly connected nodes tend to be connected with other high degree nodes.
Measures selected from Category IV: M16, Radial Centric Information Index; M17, Compactness Measure Based on Distance Degrees; M18, Complexity Index B. All these measures refer to entropy, information and other complexity in the network. Radial Centric Information Index and Compactness Measure Based on Distance Degrees are both information-theoretic measures to determine the structural information content of a network, and both of them are based on Shannon’s entropy. Complexity Index B is a more recently developed measure due to Bonchev [39]. The complexity index bv is the ratio of the vertex degree and its distance degree. The sum over all bv indices is the convenient measure of network complexity, i.e., the complexity index B.
A systematic discussion about the topological measures in complex networks is out of the scope of this paper. Detailed description of these measures can be found in [4,18,40,41].
Besides the 18 topological measures mentioned above, we also track two performance measures, i.e. “P01: Technological Volume” and “P02: Contract Turnover”, which will be described in Section 2.3.2.
2.2.2. Drive-response Network Inference
The drive-response network to be constructed can be denoted as G=(V,E), here, V={V1,V2,…,Vn} is the set of vertices/nodes, i.e., the measures, and E is the set of edges, i.e., pair-wise relations between any two measures. The adjacency matrix A of the drive-response network is defined as follows:
The Transfer Entropy from a time series Y to a times series X as the average information contained in the source Y about the next state of the destination X that was not already contained in the destination’s past [31,35]:
Though the analytic form of transfer entropy is relatively simple, but its application to investigation on time series of topological measures is not so easy. There are five major practical challenges:
Time series being non-stationary: The probabilities are estimated from observations of a single instance over a long time series. It is very important therefore that the time series is statistically stationary over the period of interest, which can be a practical problem with transfer entropy calculations [42]. In most cases the time series of topological measures are non-stationary.
Time series being continuous: It is problematic to calculate the transfer entropy on continuous-valued time series such as we have here. Kaiser and Schreiber developed a criticism and presented many caveats to the extension of the transfer entropy to continuous variables [43]. Here we will resort to another solution.
Finite sample effects: A finite time series will result in fewer examples of each combination of states from which to calculate the conditional probabilities. When used to analyze finite experimental time series data, there is a strong risk of overestimating the influence, a problem that is known from the literatures [44,45].
Indirect effects: When evaluating the influence between two time series from a multivariate data set, the case in our study, it is necessary to take the effects of the remaining variables into account, and distinguish between direct and indirect effects [46].
Statistical significance: A small value of transfer entropy suggests no relation while a large value does. Two irrelevant series can have non-zero transfer entropy due to finite sample size of the time series [47], thus it is not a good choice to simply select a threshold value to judge whether there exists drive-response relationship between two measures.
In the last few years, several improved transfer entropy algorithms have been proposed to deal with some of these challenges. For example, Symbolic Transfer Entropy [48] is a solution for (1) and (2), Effective Transfer Entropy [44] is for (3), while Partial Transfer Entropy [49] is for (4). In order to deal with these practical challenges all at once, techniques from Symbolic Transfer Entropy, Effective Transfer Entropy, and Partial Transfer Entropy should be synthesized, resulting an effective, partial, symbolic version of Transfer Entropy as follows:
Let us consider {v1,t}, {v2,t}, t=1,2,⋯k as the denotations for the time series of measures v1 and v2 respectively. The embedding parameters in order to form the reconstructed vector of the time series of v1 are the embedding dimension m1 and the time delay τ1. The reconstructed vector of v1 is defined as:
The reconstructed vector for v2 is defined accordingly, with parameters m2 and τ2. For each vector v1,t, the ranks of its components assign a rank-point where for j=1,⋯,m1, and is defined accordingly.
The symbolic transfer entropy is defined as [48]:
The partial symbolic transfer entropy is defined conditioning on the set of the remaining time series z={v3,v4,⋯,vN}.
Finally, we will define effective partial symbolic transfer entropy as follows:
By now, we have coped with the practical challenges (1), (2), (3) and (4) with effective partial symbolic transfer entropy. For challenge (5), i.e., statistical significance, it may be evaluated by using bootstrapping strategies, surrogate data or random permutations [50,51]. Under the surrogate-based testing scheme, we will assess the significance with kernel density estimation.
By shuffling the time series for M times, we now get M different values and we will denote them as p1, p2,…,pM, and we denote as p0. We build with M+1 values a probability distribution function using a kernel approach, known as Parzen-Rosenblat method [52,53], which can be expressed as:
The existence of a drive-response link between two measures is then determined using this probability and a pre-defined significant level. The final , a21, is defined as:
Other entries aij in the adjacency matrix A can be calculated in the same way.
2.2.3. Drive-response Network Analysis
The resulting network can be analyzed from a two-fold perspective:
At the local node level, we are going to calculate the in-strength and out-strength [55] of each node to assess how influential and comprehensive it is:
In the context of drive-response relationships, the specific implications of the in-strength and out-strength are: the out-strength is the sum of information flowing from the measure to others, which stands for its prestige and reveals its influence to others. The in-strength is the sum of information flowing from others to the measure. The greater the in-strength a measure has, the more comprehensive the measure is, since there are more information flows to it from other measures.
On the global network level, we are going to cluster the measures into different groups by detecting communities in the resulting network. Measures in the same community are clustered into one group. If the resulting network is complicated, tools for detecting communities in the network science can be employed.
2.3. Further Remarks
2.3.1. Choice of Coupling Measure
In fact, the choice of coupling measure between pairs of time series permits many alternatives, ranging from correlation and partial correlation to mutual information and causality measures [56], with the cross correlation [57] and Granger causality [58] being the famous ones. Some of these popular tools are non-directional, e.g. correlation or partial correlation, and mutual information measures, thus these measures cannot provide satisfactory results for our study since the interactions between the measures are not necessarily symmetric. Granger causality has acquired preeminent status in the study of interactions and is able to detect asymmetry in the interaction. However, its limitation is that the model should be appropriately matched to the underlying dynamics of the examined system, otherwise model misspecification may lead to spurious causalities [46]. Given a complex system with a priori unknown dynamics, the first choice might be Transfer Entropy [59]. Its advantages are obvious: (1) it makes minimal assumptions about the dynamics of the time series and does not suffer from model misspecification bias; (2) it can captures both linear and nonlinear effects; (3) it is numerically stable even for reasonably small sample sizes [60].
2.3.2. Validation of the Proposed Method
The proposed method is an integration of techniques from Symbolic Transfer Entropy, Effective Transfer Entropy, and Partial Transfer Entropy. All these relevant techniques have been proved theoretically and practically by numerical simulation and empirical investigations, respectively in [44,48,49], and these techniques are compatible, which means they can be synthesized to provide more comprehensive solutions. In fact, there already exist some synthesized methods such as Partial Symbolic Transfer Entropy [46], Corrected Symbolic Transfer Entropy with surrogate series to make the results more effective [61], and Effective Transfer Entropy based on symbolic encoding techniques [62]. To our best knowledge, research taking into account of all these five practical issues mentioned above and synthesizing all these techniques all at once still lacks.
Since our investigation is applied here to purely observational data, we have no way to validate the proposed framework with simulated signals or outside intervention. To valid the feasibility of the proposed method, we will resort to another strategy which is based on experiential evidence:
Suppose that the relationship between the topological measures here and some other measures are experientially approved. We then embed these extra measures into our data, deduce the drive-response relationship between these extra measures and the topological measures, and test if the results of our proposed method are consistent with the existing knowledge. Obviously the consistence will give us more confidence on the feasibility of our method.
Here, the extra measures are two performance indices of technology exchange, i.e., P01: Technological Volume and P02: Contract Turnover, which have been adopted by BTMMO for several years [63]. In the context of System Theory, it is generally believed that system structure determines its function/the performance. Thus, what is expected is that these two embedded measures will be responding ones while some of the topological measures will drive them.
3. Empirical Application and Results
3.1. Time Series of Topological Measures in Technology Exchange Network
Technology exchange holds a great potential for promoting innovation and competitiveness at regional and national levels [64]. In order to expedite scientific and technological progress and innovation, it is stipulated in the Regulation of Beijing Municipality on Technology Market that the first party of the contract can get tax relief if the contract is identified as a technique-exchanging one and registered by BTMMO. Because of the preferential taxes, most of the technology exchange activities are recorded by BTMMO, in the form of technology contracts. Thus it offers the chance for us to obtain high-quality technology exchange records from BTMMO. We are able to capture the total evolutional scenario of the Technology Exchange Network.
Networks serve as a powerful tool for modeling the structure of complex systems, and there is no exception for technology exchange. Intuitively we can model technology exchange as a network with the contracting parties as the nodes and contracts as the edges which linking the two contracting parties together. However, in the complex network literature, it is often assumed that no self-connections or multiple connections exist [4]. In other words, we will model the technology exchange as a simple graph as follows: we take the contracting parties as the nodes, and if contractual relationship between any two parties exists, regardless of how many contracts they signed, there will be (only) one edge linking them together. Here, the resulting technology exchange network is treated as an undirected and un-weighted one.
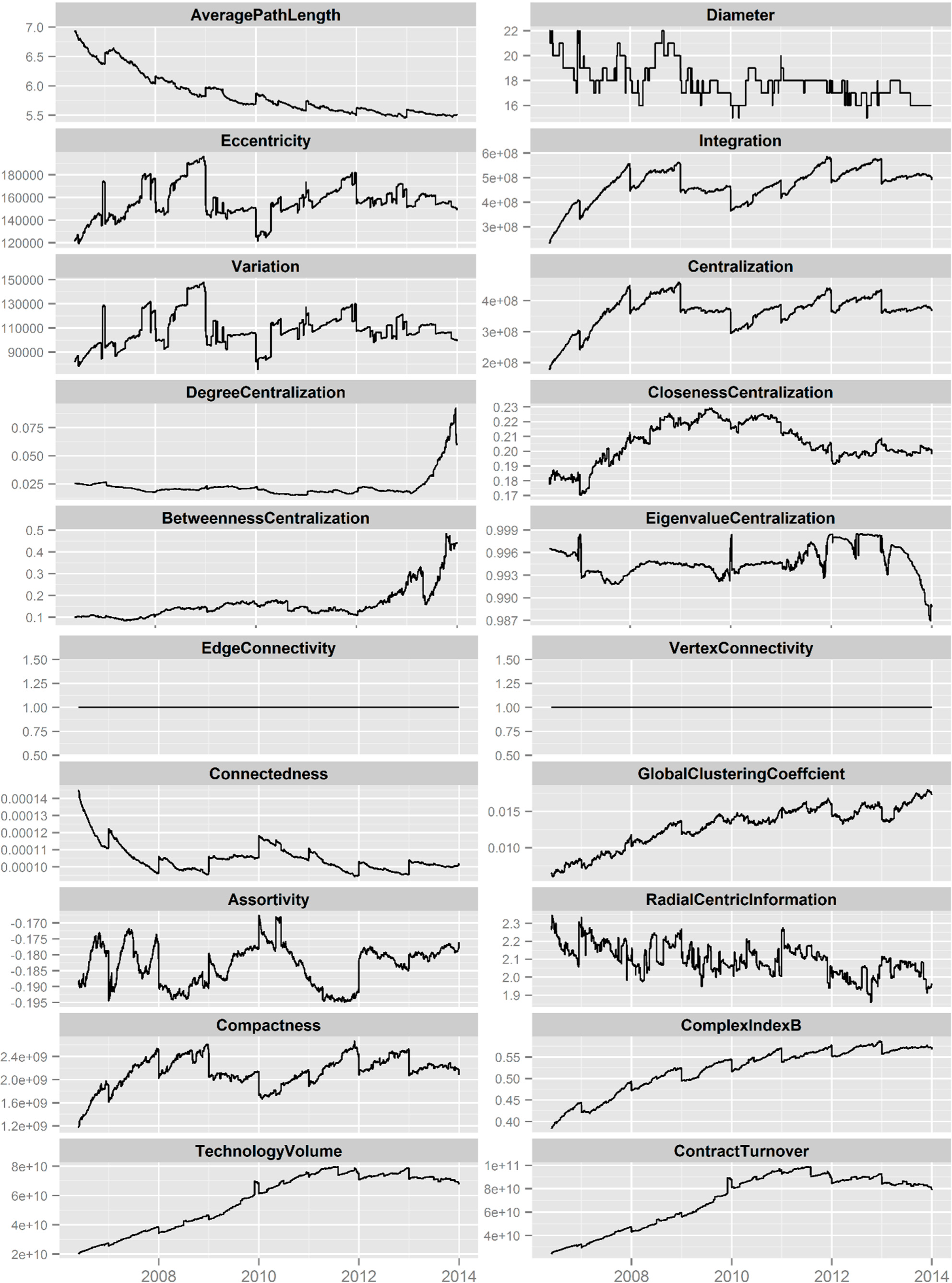
We observed the 18 topological and two performance measures of the Technology Exchange Network in Beijing day by day from 24 May 2006 to 31 December 2013, obtaining 2779 records in total. This is the most fine-grained data that we can get, because technology exchange activities can only be accurate at the day level, rather than to hours or seconds as in stock exchanges. The complete dataset is provided as a supplementary.
Since the technology exchange network is not a connected one, all the measures are calculated on the giant component of these networks. The measures M01, M02, M07, M08, M09, M10, M11, M12, M13, M14, M15 are calculated with the igraph packages [41], while measures M03, M04, M05, M06, M16, M17, M18 are calculated by the QuACN package [40]. All these algorithms are implemented in the R language [65], and we visualize our results mainly with the ggplot2 package [66]. The time series of all these measures are shown in Figure 2.
3.2. Drive-Response Network Inference and Analysis
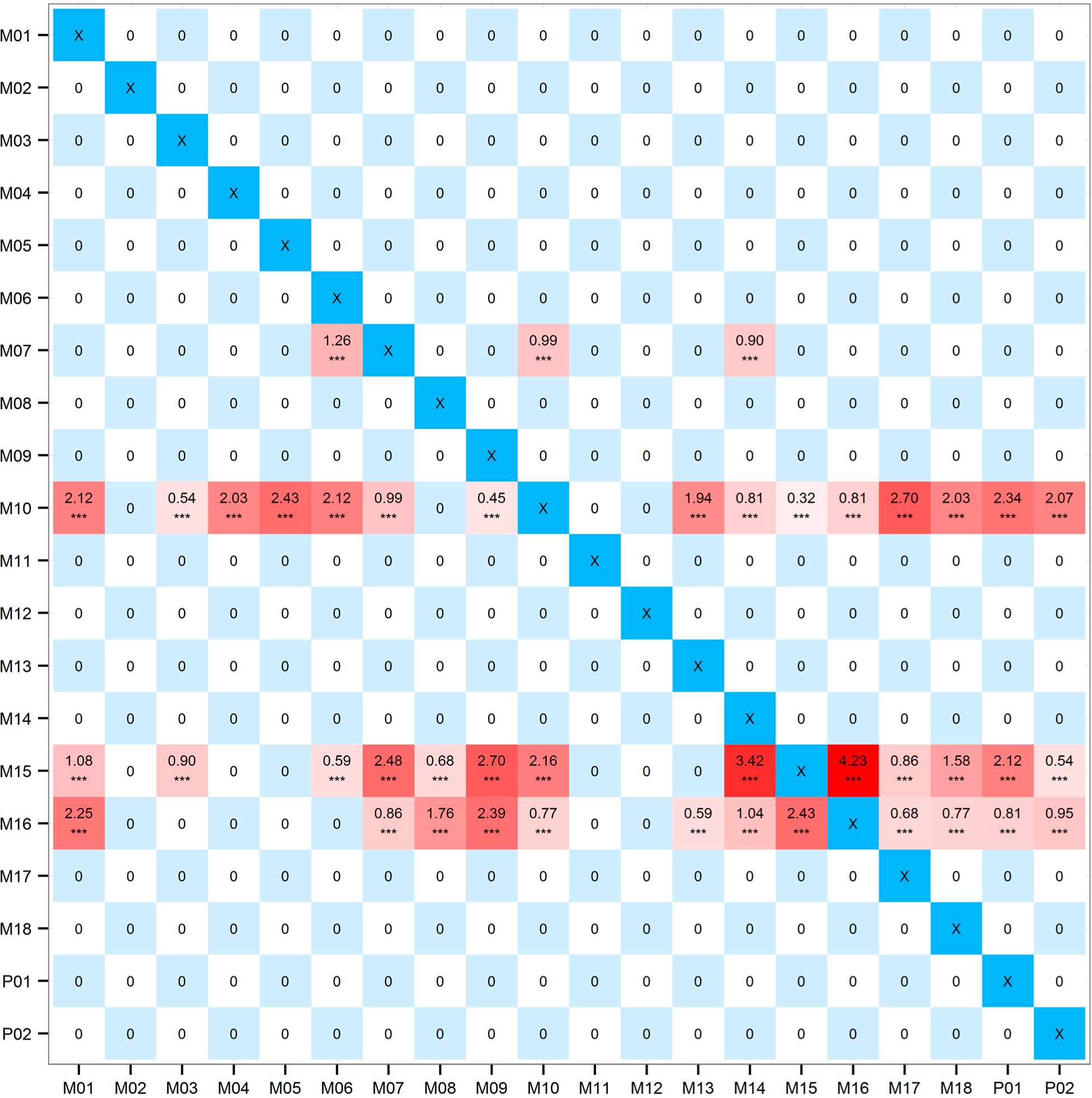
Calculating the time series depicted in Section 3.1 with the method proposed in Section 2.2.2, we get the adjacent matrix, which is shown in Figure 3 (Since the EPSTE values are rather small, all the entries are multiplied by 10,000 for ease of plotting).
In Figure 3, the diagonal entries are marked with “X” because we will not study the self-correlations and these entries are omitted. Red-filled entries are not only greater than zero but also statistically significant, thus each red-filled entry stands for a drive-response relationship. The darker the color, the more significant the relationship is. It can be seen that the darkest entries are all located in row M07, M10, M15, and M16, which means the strong drive-response relationships share these four common drives. We will further analyze these rows after constructing the drive-response network.
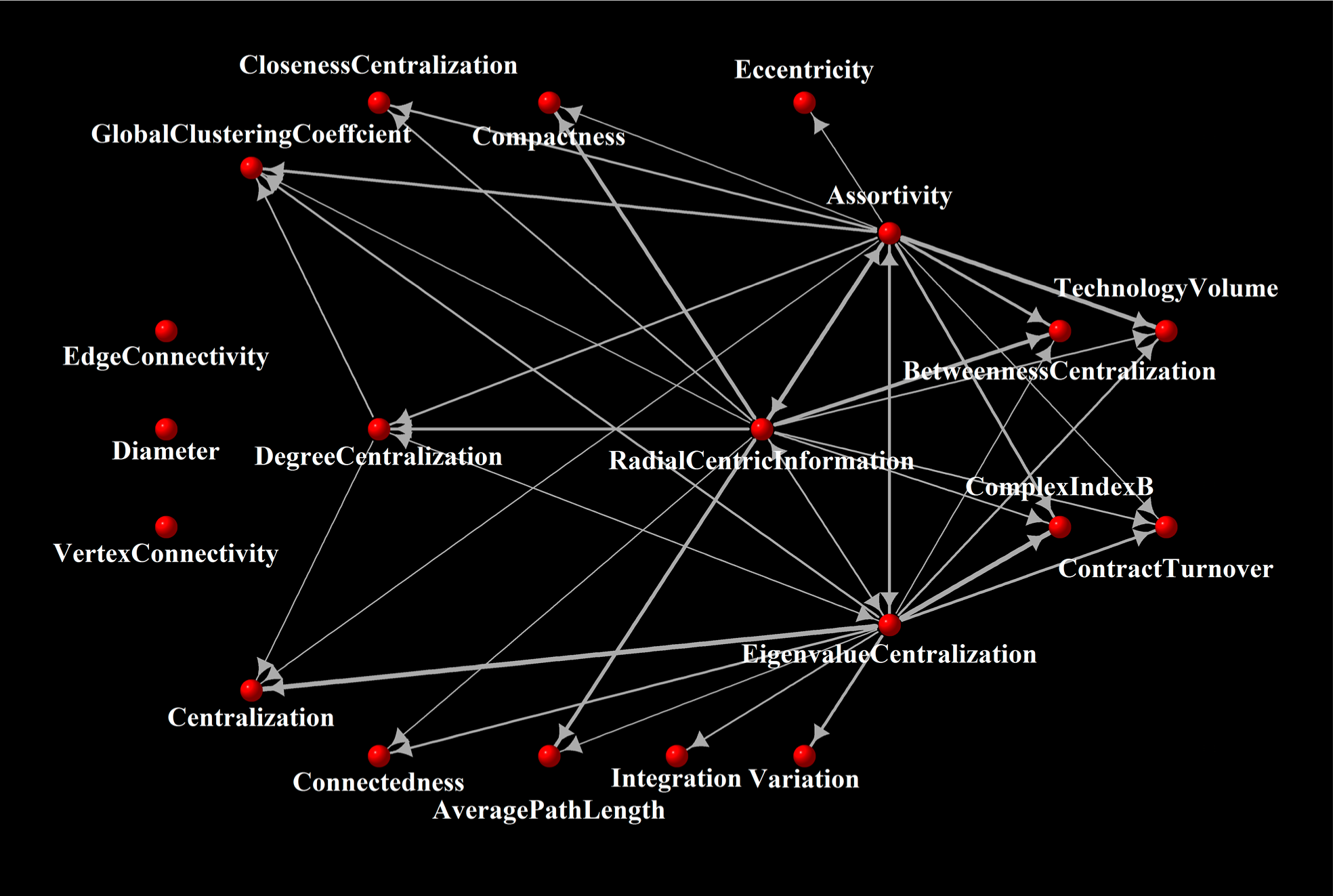
Finish the steps proposed in Section 2.2.3, and we can draw the drive-response network, which is shown in Figure 4. In Figure 4, each measure is mapped as a node, and each arrow stands for a drive-response relationship, and we associate each edge with a weight value, i.e., the effective partial symbolic transfer value, which is mapped as the width of the lines.
Some basic features of the resulting network can be mentioned: there are 20 nodes and 43 edges in the network. The connectedness is 0.1131579, with the average vertex degree 4.3. It can been seen that the resulting network is not a connected one, with three isolated measures which are relatively independent.
Although most of the vertices are connected, it is certainly not a dense graph. The diameter of giant component of the resulting is 3, and the average path length is 1.34375. Thus, the information flowing on this network is relatively simple. Further investigation on the drive-response network is two-fold. On the one hand, we will calculate the out-strength and in-strength of each measure to uncover how influential and comprehensive it is. On the other hand, we will cluster the measures into different groups. The out-strength and in-strength values of each measure is shown in Table 2.
It can be seen from Table 2 that the most influential measures are Eigenvalue Centralization, Assortativity Coefficient, Radial Centric Information and Degree Centralization. Among these measures, two of them are centralization measures, one is connection measure and the remaining other is entropy measure. There is no distance relevant measure to be influential ones. In other words, distance relevant measures are usually driven by others. Graph integration, variation, eccentricity and average path length are influenced by the graph assortativity and eigenvalue centralization.
It can also be seen from Table 2 that measure M14: Global Clustering Coefficient is the most comprehensive one since it takes up the most information from others. Another popular measure M01: Average Path Length, also has a relatively great in-strength value. These two measures are often employed to characterize and class networks [1,4]. Except the three isolated measures, the in-strength values of all the other measures are greater than zero, which implies that most measures are influenced by others.
According to the network structure, we can cluster the 18 measures into three groups:
Driving measures:
M07, Degree Centralization;
M10, Eigenvalue Centralization;
M15, Assortativity Coefficient;
M16, Radial Centric Information.
Responding measures:
M01, Average Path Length;
M03, Eccentricity;
M04, Integration;
M05, Variation;
M06, Centralization;
M08, Closeness Centralization;
M09, Betweenness Centralization;
M13, Connectedness;
M14, Global Clustering Coefficient;
M17, Compactness;
M18: Complexity Index B.
Standalone measures:
M02, Diameter;
M11, Vertex Connectivity;
M12, Edge Connectivity.
The isolation implies that these measures have no information flow with other measures. It doesn’t mean that these measures are trivial ones; rather, they should be treated as non-redundant ones because they contain special information that is not include by other measures, indicating that some of them may reveal different topological aspects of real-world networks.
Now, we will tend to the two embedding measures: “P01, Technological Volume” and “P02, Contract Turnover”. In our resulting network, both the two are identified as responding measures, which is consistent with the principle of System Theory that “The structure of the system determines its function”. Further, the in-strength value of “P01, Technological Volume” (0.0005268372) is greater than that of “P02, Contract Turnover” (0.0003557277). This result is also consistent with our experience that what we are investigating on is the technology exchange network, it stands to reason that the technological volume gains more information from its own structure. Both these two results can serve as evidence for the feasibility of our proposed method.
4. Conclusions and Discussions
Taking into account that pulling networks from different domains and topologies together for statistical analysis might provide incorrect conclusions [25], we conduct our investigation with the data observed from the same network in the form of simultaneously measured time series. In order to reveal the relationships among topological measures from their time series, we synthesize a practical framework comprising techniques from Symbolic Transfer Entropy, Effective Transfer Entropy, and Partial Transfer Entropy, which is able to deal with the challenges such as time series being non-stationary, time series being continuous, finite sample effects and indirect effects. Using a surrogate-based testing scheme, we assess the statistical significance of the resulting drive-response relationships with kernel density estimation. Thus, the synthesized framework can serve as a complete solution for the application of transfer entropy in complicated issues. Furthermore, the framework doesn’t stop at the pair-wise relationships, but makes further efforts to provide a holistic scenario in the form of a drive-response network. The transfer entropy-based framework not only quantifies the pair-wise influence one measures exerts on another, but also reveals the overall structure of the measures.
We select 18 topological measures and apply the proposed method to the empirical investigation on Technology Exchange Network. After calculating the drive-response relationships and inferring the network of these measures, we identify the most influential and most comprehensive measures according to their in-strength and out-strength values. We also cluster these measures into three groups, i.e., driving measures, responding measures, and standalone measures. By embedding two performance measures, i.e., technological volume and contract turnover and calculating the relationships between topological and performance measures, we find that our results are consistent with the principle of System Theory and some existing knowledge, which validates the feasibility of our proposed method.
Our conclusion is based on the purely observational data from Technology Exchange Network in Beijing, thus the resulting drive-response network should not be simply generalized. In other words, the drive-response network may not hold true for other networks. However, the proposed method is applicable to other types of network, in case that the time series of topological measures in that network can be observed.
It is to be mentioned that although we can divide the measures into driving and responding ones, it is not to say that the driving measures can determine the responding measures. The drive-response relationships are not equal to deterministic relationships. In general, approaches based on observational quantities alone are not able to disclose a deterministic picture of the system, and interventional techniques will ultimately be needed. Nevertheless, the proposed method can serve as a heuristic tool in detecting directed information transfer, and the detected drive-response relationships can be viewed as a justifiable inferential statistic for true relationships, which give us more evidence and confidence to reveal intrinsic relationship among the topological measures.
Acknowledgments
We are grateful to Beijing Technology Market Management Office for its permission to collect data from Beijing Technical Contract Registration System. The authors would like to thank the two anonymous reviewers for their valuable comments and suggestions to improve the quality of the paper.
PACS Codes: 05.45.Tp; 05.90.+m
Conflicts of Interest
The author declares no conflict of interest.
References
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 393, 440–442. [Google Scholar]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar]
- Costa, L.D.F.; Oliveira, O.N.; Travieso, G.; Rodrigues, F.A.; Boas, P.R.V.; Antiqueira, L.; Viana, M.P.; Rocha, L.E.C. Analyzing and modeling real-world phenomena with complex networks: A survey of applications. Adv. Phys. 2011, 60, 329–412. [Google Scholar]
- Costa, L.D.F.; Rodrigues, F.A.; Travieso, G.; Boas, P.R.V. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar]
- Koç, Y.; Warnier, M.; van Mieghem, P.; Kooij, R.E.; Braziera, F.M.T. A topological investigation of phase transitions of cascading failures in power grids. Physica A 2014, 415, 273–284. [Google Scholar]
- Peres, R. The impact of network characteristics on the diffusion of innovations. Physica A 2014, 402, 330–343. [Google Scholar]
- Lee, D.; Kim, H. The effects of network neutrality on the diffusion of new Internet application services. Telemat. Inform. 2014, 31, 386–396. [Google Scholar]
- Albert, R.; DasGupta, B.; Mobasheri, N. Topological implications of negative curvature for biological and social networks. Phys. Rev. E 2014, 89. [Google Scholar] [CrossRef]
- Hernández, J.M.; van Mieghem, M. Classification of graph metrics, Available online: http://naseducation.et.tudelft.nl/images/stories/javier/report20110617_Metric_List.pdf accessed on 2 October 2014.
- Estrada, E.; de la Pena, J.A.; Hatano, N. Walk entropies in graphs. Linear Algebr. Appl. 2014, 443, 235–244. [Google Scholar]
- Topirceanu, A.; Udrescu, M.; Vladutiu, M. Network fidelity: A metric to quantify the similarity and realism of complex networks, Proceedings of the Third International Conference on Cloud and Green Computing, Karlsruhe, Germany, 30 September–2 October 2013.
- Vianaa, M.P.; Fourcassié, V.; Pernad, A.; Costa, L.D.F.; Jost, C. Accessibility in networks: A useful measure for understanding social insect nest architecture. Chaos Solitons Fractals 2013, 46, 38–45. [Google Scholar]
- Bearden, K. Inferring complex networks from time series of dynamical systems: Pitfalls, misinterpretations, and possible solutions 2012, arXiv, 1208.0800.
- Jamakovic, A.; Uhlig, S. On the relationships between topological metrics in real-world networks. Netw. Heterog. Media (NHM) 2008, 3, 345–359. [Google Scholar]
- Krioukov, D.; Chung, F.; Claffy, K.C.; Fomenkov, M.; Vespignani, A.; Willinger, W. The workshop on internet topology (WIT) report. Comput. Commun. Rev. 2007, 37, 69–73. [Google Scholar]
- Barrat, A.; Barthelemy, M.; Vespignani, A. Dynamical Processes on Complex Networks; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Barrat, A.; Weigt, M. On the properties of small-world network models. Eur. Phys. J. B 2000, 13, 547–560. [Google Scholar]
- Chen, G.; Wang, X.; Li, X. Introduction to Complex Networks: Models, Structures and Dynamics; Higher Education Press: Beijing, China, 2012. [Google Scholar]
- Cohen, R.; Havlin, S. Scale-free networks are ultrasmall. Phys. Rev. Lett. 2003, 86, 3682–3685. [Google Scholar]
- Chicharro, D.; Ledberg, A. Framework to study dynamic dependencies in networks of interacting processes. Phys. Rev. E 2012, 86. [Google Scholar] [CrossRef]
- Li, C.; Wang, H.; de Haan, W.; Stam, C.J.; van Mieghem, P. The correlation of metrics in complex networks with applications in functional brain networks. J. Stat. Mech. Theory Exp. 2011, 11. [Google Scholar] [CrossRef]
- Roy, S.; Filkov, V. Strong associations between microbe phenotypes and their network architecture. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef]
- Filkov, V.; Saul, Z.; Roy, S.; D’Souza, R.M.; Devanbu, P.T. Modeling and verifying a broad array of network properties. Europhys. Lett. (EPL) 2009, 86. [Google Scholar] [CrossRef]
- Garcia-Robledo, A.; Diaz-Perez, A.; Morales-Luna, G. Correlation analysis of complex network metrics on the topology of the Internet, Proceedings of the International Conference and Expo. on Emerging Technologies for a Smarter World, Melville, NY, USA, 21–22 October 2013.
- Bounova, G.; de Weck, O. Overview of metrics and their correlation patterns for multiple-metric topology analysis on heterogeneous graph ensembles. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.; van Mieghem, P.; Stanley, H.E.; Wang, H. Correlation between centrality metrics and their application to the opinion model 2014, arXiv, 1409.6033.
- Sun, X.; Wandelt, S. Network similarity analysis of air navigation route systems. Transp. Res. E 2014, 70, 416–434. [Google Scholar]
- Lin, J.; Ban, Y. The evolving network structure of US airline system during 1990–2010. Physica A 2014, 410, 302–312. [Google Scholar]
- Tung, T.Q.; Ryu, T.; Lee, K.H.; Lee, D. Inferring gene regulatory networks from microarray time series data using transfer entropy, Proceedings of the IEEE International Symposium on Computer-Based Medical Systems, Maribor, Slovenia, 20–22 June 2007.
- Albano1, A.M.; Brodfuehrer, P.D.; Cellucci, C.J.; Tigno, X.T.; Rapp, P.E. Time series analysis, or the quest for quantitative measures of time dependent behavior. Philipp. Sci. Lett. 2008, 1, 18–31. [Google Scholar]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar]
- Vejmelka, M.; Paluš, M. Inferring the directionality of coupling with conditional mutual information. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef]
- Wu, J.; Di, Z. Complex network in statistical physics. Prog. Phys. 2004, 24, 18–46. [Google Scholar]
- Timme, M.; Casadiego, J. Revealing networks from dynamics: An introduction. J. Phys. A 2014, 47. [Google Scholar] [CrossRef]
- Sandoval, L. Structure of a global network of financial companies based on transfer entropy. Entropy 2014, 16, 4443–4482. [Google Scholar]
- Durek, P.; Walther, D. The integrated analysis of metabolic and protein interaction networks reveals novel molecular organizing principles. BMC Syst. Biol. 2008, 2. [Google Scholar] [CrossRef]
- Rubina, T. Tools for analysis of biochemical network topology. Biosyst. Inf. Technol. 2012, 1, 25–31. [Google Scholar]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1979, 1, 215–239. [Google Scholar]
- Bonchev, D.; Rouvray, D.H. Complexity in Chemistry, Biology, and Ecology; Springer: New York, NY, USA, 2005. [Google Scholar]
- Mueller, L.A.J.; Kugler, K.G.; Dander, A.; Graber, A.; Dehmer, M. QuACN: An R package for analyzing complex biological networks quantitatively. Bioinformatics 2011, 27, 140–141. [Google Scholar]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJ. Complex Syst. 2006, 1695. Available online: http://www.necsi.edu/events/iccs6/papers/c1602a3c126ba822d0bc4293371c.pdf accessed on 28 October 2014. [Google Scholar]
- Thorniley, J. An improved transfer entropy method for establishing causal effects in synchronizing oscillators, Proceedings of the Eleventh European Conference on the Synthesis and Simulation of Living Systems, Winchester, UK, 5–8 August 2008.
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Physica D 2002, 166, 43–62. [Google Scholar]
- Marschinski, R.; Kantz, H. Analysing the information flow between financial time series. Eur. Phys. J. B 2002, 30, 275–281. [Google Scholar]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar]
- Diks, C.G.H.; Kugiumtzis, D.; Kyrtsou, K.; Papana, A. Partial Symbolic Transfer Entropy; CeNDEF Working Paper 13–16; University of Amsterdam: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Jo, S. Computational Studies of Glycan Conformations in Glycoproteins. Ph.D. Thesis, University of Kansas, Lawrence, KS, USA, 31 May 2013. [Google Scholar]
- Staniek, M.; Lehnertz, K. Symbolic transfer entropy. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef]
- Vakorin, V.A.; Krakovska, O.A.; McIntosh, A.R. Confounding effects of indirect connections on causality estimation. J. Neurosci. Methods 2009, 184, 152–160. [Google Scholar]
- Amblard, P.O.; Michel, O.J.J. On directed information theory and Granger causality graphs. J. Comput. Neurosci. 2010, 30, 7–16. [Google Scholar]
- Good, P.I. Permutation, Parametric and Bootstrap Tests of Hypotheses, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Rosenblatt, M. Remarks on some nonparametrice stimates of a density function. Annal. Inst. Stat. Math. 1956, 27, 832–837. [Google Scholar]
- Parzen, E. On estimation of a probability density function and mode. Annal. Inst. Stat. Math. 1962, 33, 1065–1076. [Google Scholar]
- Sheather, S.J.; Jones, M.C. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. 1991, 53, 683–690. [Google Scholar]
- Guo, S.; Lu, Z.; Chen, Z.; Luo, H. Strength-strength and strength-degree correlation measures for directed weighted complex network analysis. IEICE Trans. Inf. Syst. 2011, E94-D, 2284–2287. [Google Scholar]
- Kramer, M.A.; Eden, U.T.; Cash, S.S.; Kolaczyk, E.D. Network inference with confidence from multivariate time series. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef]
- Gozolchiani, A.; Yamasaki, K.; Gazit, O.; Havlin, S. Pattern of climate network blinking links follows El Niño events. Europhys. Lett. (EPL) 2008, 83. [Google Scholar] [CrossRef]
- Granger, C.W.J. Some aspects of causal relationships. J. Econom. 2003, 112, 69–71. [Google Scholar]
- Lungarella, M.; Ishiguro, K.; Kuniyoshi, Y.; Otsu, N. Methods for quantifying the causal structure of bivariate time series. Int. J. Bifurcat. Chaos 2007, 17, 903–921. [Google Scholar]
- Lungarella, M.; Sporns, O. Mapping information flow in sensorimotor networks. Comput. Biol. 2006, 2. [Google Scholar] [CrossRef]
- Chernihovskyi, A. Information-theoretic approach for the characterization of interactions in nonlinear dynamical systems. 2011, urn:nbn:de:hbz:5N-25132; Universitäts-und Landesbibliothek Bonn. Available online: http://hss.ulb.uni-bonn.de/2011/2513/2513.htm accessed on 19 August 2014.
- Peter, F.J.; Dimpfl, T.; Huergo, L. Using transfer entropy to measure information flows between financial markets. Proceedings of Midwest Finance Association 2012 Annual Meetings, New Orleans, LA, USA, 22–25 February 2012.
- 2012 Report of Beijing Technology Market; Beijing Technology Market Management Office: Beijing, China, 2012.
- Bennett, D.J.; Vaidya, K.G. Meeting technology needs of enterprises for national competitiveness. Int. J. Technol. Manag. 2005, 32, 112–153. [Google Scholar]
- R Core Team, R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014.
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2009. [Google Scholar]
| ID | Name | Definition | Ref. |
|---|---|---|---|
| I. Distance Relevant Measures | |||
| M01 | Average Path Length | , here N denotes the number of the nodes, and d(u,v) denotes the steps along the shortest path between nodes u and v | [18] |
| M02 | Diameter | [18] | |
| M03 | Eccentricity | , here, d(u,v) stands for the distances between u,v ∊ N (G) | [40] |
| M04 | Integration | , here, D(v) is the vertex centrality which is defined as | [40] |
| M05 | Variation | , here, ΔD*(v) is the distance vertex deviation ΔD* (v):= D(v)−D*(G) | [40] |
| II. Centralization Measures | |||
| M06 | Centralization | , here ΔD* (v) is the distance vertex deviation which is defined as ΔD* (v):= D(v)−D*(G) | [40] |
| M07 | Degree Centralization * | , here CD(v) is the degree centrality of vertex v, , and kv is the vertex degree | [41] |
| M08 | Closeness Centralization * | , here CC(v) is the closeness centrality of vertex v, | [41] |
| M09 | Betweenness Centralization * | , here CB(v) is the closeness centrality of vertex v, which is defined as , and gu,w is the number of paths connecting u and w, gu,w (v) is the number of paths that v is on | [41] |
| M10 | Eigenvector Centralization* | , here CE(v) is the centrality of vertex v, which can be calculated by the formula , and the vector of the centralities of vertices is the eigenvector of adjacency matrix A=(aij) | [41] |
| III. Connection Measures | |||
| M11 | Vertex Connectivity | κ(G):= min {κ(u,v)∣ unordered pair u, v ∊ N (G)}, here, κ(u, v) is defined as the least number of vertices, chosen from N (G)−{u, v}, whose deletion from G would destroy every path between u and v | [41] |
| M12 | Edge Connectivity | λ (G):= min{λ (u,v)| unordered pair u, v ∊ N (G)}, here, λ(u,v) is the least number of edges whose deletion from G would destroy every path between u and v | [41] |
| M13 | Connectedness | , here A(G) is the index of total adjacency and aij is the entry lies in row i and column j in the adjacent matrix A=(aij) | [40] |
| M14 | Global Clustering Coefficient | , where, (VN(v), EN(v)) is the sub-graph of G that contains all neighborhood vertices and their edges | [18] |
| M15 | Assortativity Coefficient | , here, M is the total number of edges, and aij is the entry lies in row i and column j in the adjacent matrix A=(aij) | [4] |
| IV. Entropy and Other Complexity Measures | |||
| M16 | Radial Centric Information Index | , here, is the number of vertices having the same eccentricity | [40] |
| M17 | Compactness Measure Based on Distance Degrees | here, W is the Wiener Index and qk is the sum of the distance degrees of all vertices located at a topological distance of k from the center of the graph | [40] |
| M18 | Complexity Index B | . Here, bi is the ratio of the vertex degree kv and its distance degree | [40] |
*In our study some of the centralization measures are normalized by dividing by the maximum theoretical score for a graph with the same number of vertices. For degree, closeness and betweenness the most centralized structure is an undirected star. For eigenvector centrality the most centralized structure is the graph with a single edge.
| ID | Measure | Out-strength | In-strength |
|---|---|---|---|
| M01 | Average Path Length | 0.00 | 0.0005448487(#03) |
| M02 | Diameter | 0.00 | 0.00 |
| M03 | Eccentricity | 0.00 | 0.0001440922(#15) |
| M04 | Integration | 0.00 | 0.0002026297(#14) |
| M05 | Variation | 0.00 | 0.0002431556(#12) |
| M06 | Centralization | 0.00 | 0.0003962536(#08) |
| M07 | Degree Centralization | 0.0003152017(#04) | 0.0004322766(#06) |
| M08 | Closeness Centralization | 0.00 | 0.0002431556(#13) |
| M09 | Betweenness Centralization | 0.00 | 0.0005538545(#02) |
| M10 | Eigenvector Centralization | 0.0023685158(#01) | 0.0003917507(#09) |
| M11 | Vertex Connectivity | 0.00 | 0.00 |
| M12 | Edge Connectivity | 0.00 | 0.00 |
| M13 | Connectedness | 0.00 | 0.0002521614(#11) |
| M14 | Global Clustering Coefficient | 0.00 | 0.0006168948(#01) |
| M15 | Assortativity Coefficient | 0.0023324927(#02) | 0.0002746758(#10) |
| M16 | Radial Centric Information Index | 0.0015264769(#03) | 0.0005043228(#04) |
| M17 | Compactness Measure Based on Distance Degrees | 0.00 | 0.0004232709(#07) |
| M18 | Complexity Index B | 0.00 | 0.0004367795(#05) |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ai, X. Inferring a Drive-Response Network from Time Series of Topological Measures in Complex Networks with Transfer Entropy. Entropy 2014, 16, 5753-5776. https://doi.org/10.3390/e16115753
Ai X. Inferring a Drive-Response Network from Time Series of Topological Measures in Complex Networks with Transfer Entropy. Entropy. 2014; 16(11):5753-5776. https://doi.org/10.3390/e16115753
Chicago/Turabian StyleAi, Xinbo. 2014. "Inferring a Drive-Response Network from Time Series of Topological Measures in Complex Networks with Transfer Entropy" Entropy 16, no. 11: 5753-5776. https://doi.org/10.3390/e16115753




