Blind Demodulation of Chaotic Direct Sequence Spread Spectrum Signals Based on Particle Filters
Abstract
:1. Introduction
2. Problem Formulation
3. Blind Demodulation of CDS-SS Signals Based on Particle Filters
3.1. Particle Filter
3.2. Blind Demodulation of CDS-SS Signals under the White Gaussian Noises Condition
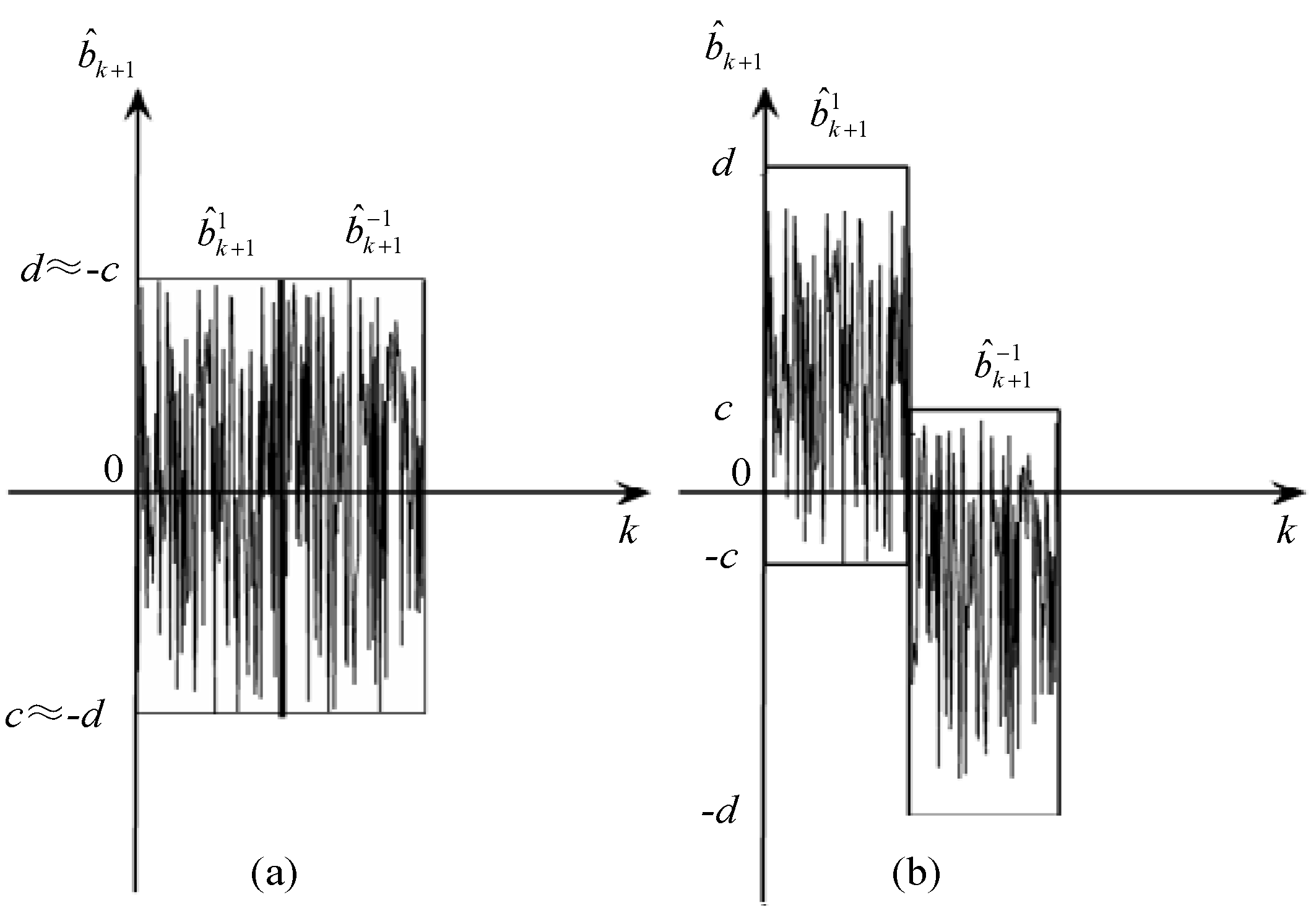
3.3. Blind Demodulation of CDS-SS Signals under Colored/Non-Gaussian Noises Condition
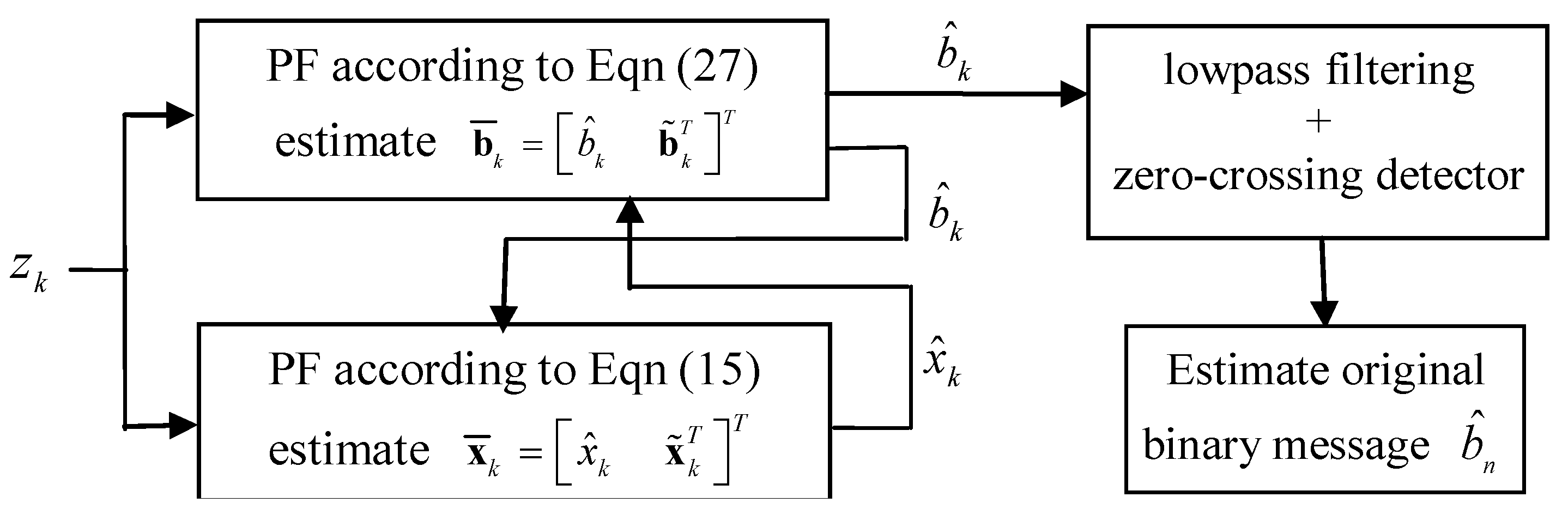
4. Simulations

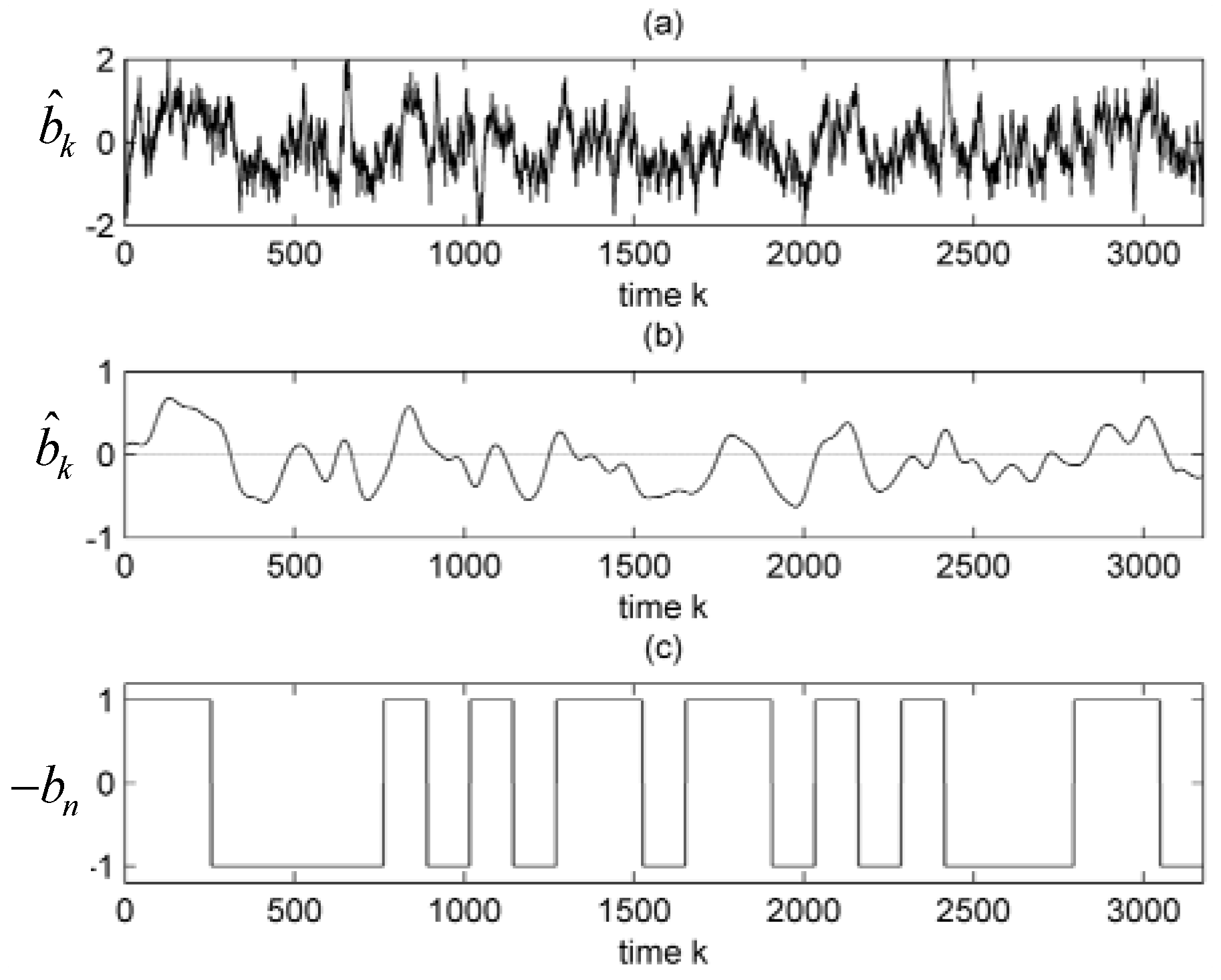
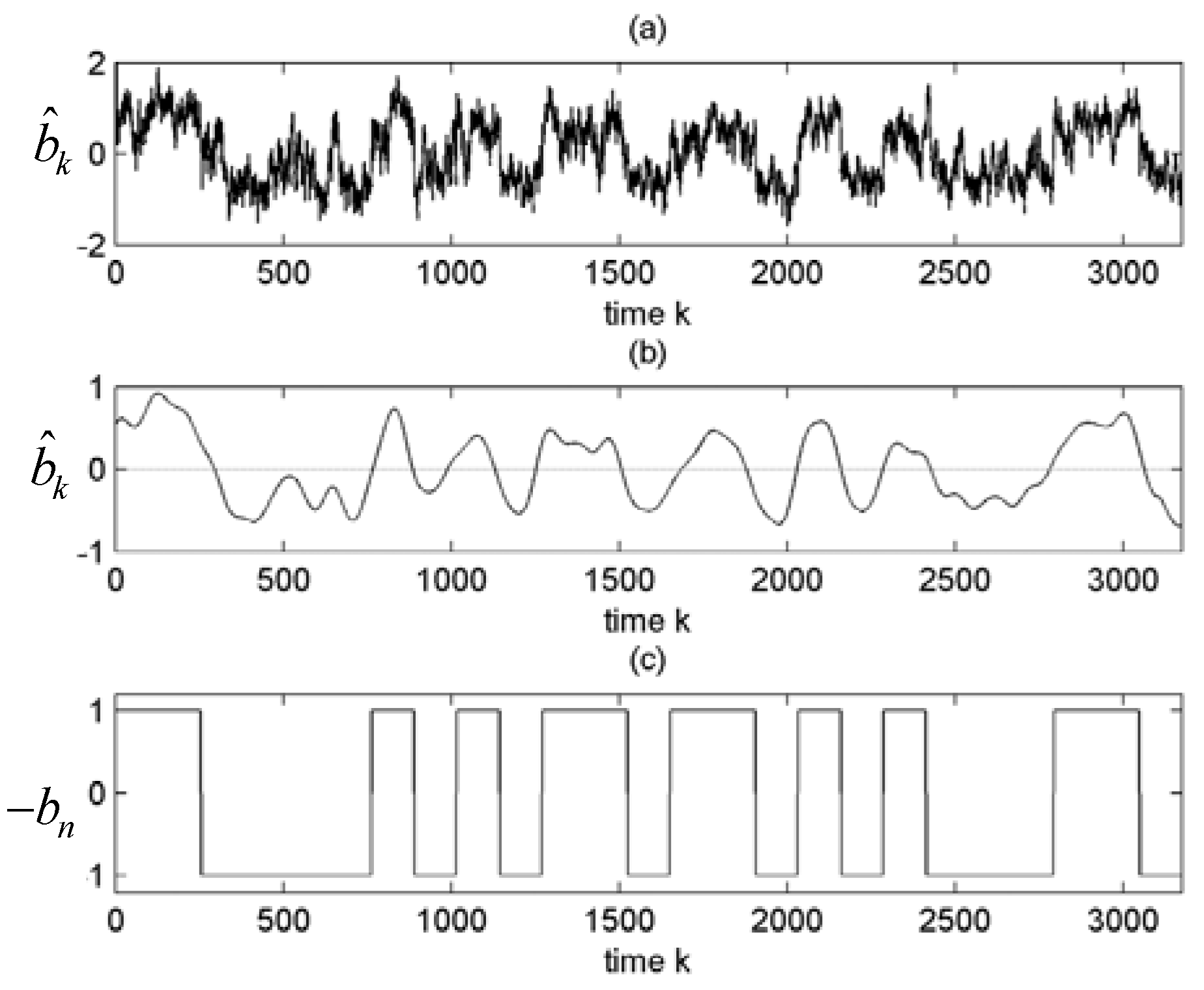
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Alvarez, G.; Montoya, F.; Romera, M.; Pastor, G. Breaking two secure communication systems based on chaotic masking. IEEE Trans. Circuits Syst. II Express Briefs 2004, 51, 505–506. [Google Scholar] [CrossRef]
- Yang, T.; Yang, L.B.; Yang, C.M. Breaking chaotic switching using generalized synchronization: Examples. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1998, 45, 1062–1067. [Google Scholar] [CrossRef]
- Alvarez, G.; Montoya, F.; Romera, M.; Pastor, G. Breaking parameter modulated chaotic secure communication system. Chaos Soliton. Fract. 2004, 21, 783–787. [Google Scholar] [CrossRef]
- Parlitz, U.; Ergezinger, S. Robust communication based on chaotic spreading sequences. Phys. Lett. A 1994, 188, 146–150. [Google Scholar] [CrossRef]
- Azou, S.; Pistre, C.; Duff, L.L.; Burel, G. Sea Trial Results of a Chaotic Direct-Sequence Spread Spectrum Underwater Communication System. In Proceedings of IEEE-OCEANS’03, San Diego, CA, USA, September 2003; pp. 1539–1546.
- Hwang, Y.; Papadopoulos, H.C. Physical-layer secrecy in AWGN via a class of chaotic DS/SS systems: Analysis and design. IEEE Trans. Signal Process. 2004, 52, 2637–2649. [Google Scholar] [CrossRef]
- Yu, J.; Yao, Y.D. Detection performance of chaotic spreading LPI waveforms. IEEE Trans. Wireless Commun. 2005, 4, 390–396. [Google Scholar]
- Sameh, M.; Ali, S.T.; Naceur, B.B. Particle Filter for State and Unknown Input Estimation of Chaotic Systems. In Proceedings of International Conference on Control, Engineering and Information Technology, Nanning, China, August 2013; pp. 67–72.
- Chen, M.; Min, W. Unknown input observer based chaotic secure communication. Phys. Lett. A 2008, 372, 1595–1600. [Google Scholar] [CrossRef]
- Dimassi, H.; Loría, A. Adaptive unknown-input observers-based synchronization of chaotic systems for telecommunication. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 800–812. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Hwang, J.P.; Kim, E. A new state estimation method for chaotic signals: Map-particle filter method. Expert Syst. Appl. 2011, 38, 11442–11446. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, W.; Fang, J.; Sun, W. Adaptive bidirectionally coupled synchronization of chaotic systems with unknown parameters. Nonlinear Dyn. 2011, 66, 67–76. [Google Scholar] [CrossRef]
- Li, X.F.; Chi, S.L.A.; Han, X.P.; Liu, X.J.; Chu, Y.D. Complete (anti-)synchronization of chaotic systems with fully uncertain parameters by adaptive control. Nonlinear Dyn. 2011, 63, 263–275. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Akbari, M.E. A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances. Appl. Math. Comput. 2012, 218, 5757–5768. [Google Scholar] [CrossRef]
- Hu, J.F.; Guo, J.B. Breaking a chaotic direct sequence spreading spectrum secure communication system. Acta Phys. Sin. 2008, 57, 1477–1484. [Google Scholar]
- Hu, J.F.; Guo, J.B. Blind estimation of chaotic spread spectrum sequences. J. Electr. Inform. Technol. 2008, 30, 1824–1827. [Google Scholar] [CrossRef]
- Xu, X.Z.; Guo, J.B. A novel unified equalization and demodulation of chaotic direct sequence spreading spectrum signal based on state estimation. Acta Phys. Sin. 2011, 60, e020510. [Google Scholar]
- Alvarez, G.; Montoya, F.; Pastor, G.; Romera, M. Breaking a secure communication scheme based on the phase synchronization of chaotic systems. Chaos 2004, 14, 274–278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luca, M.B.; Azou, S.; Hodina, E.; Serbanescu, A.; Burel, G. Pseudoblind Demodulation of Chaotic DS-SS Signals through Exact Kalman Filtering. In Proceedings of IEEE Communications Conference, Bucharest, Romania, June 2006; pp. 1–4.
- Yang, T.; Yang, L.B.; Yang, C.M. Breaking chaotic secure communication using a spectrogram. Phys. Lett. A 1998, 247, 105–109. [Google Scholar] [CrossRef]
- Hu, G.J.; Feng, Z.J.; Meng, R.L. Chosen ciphertext attack on chaos communication based on chaotic synchronization. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 275–279. [Google Scholar]
- Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation. Proc. Ins. Electr. Eng. 1993, 140, 107–113. [Google Scholar] [CrossRef]
- Shi, Z.G.; Hong, S.H.; Chen, J.M.; Chen, K.S.; Sun, Y.X. Particle filter-based synchronization of chaotic colpitts circuits combating AWGN channel distortion. Circuits Syst. Signal Process. 2008, 27, 833–845. [Google Scholar] [CrossRef]
- Watzenig, D.; Brandner, M.; Steiner, G. A particle filter approach for tomographic imaging based on different state-space representations. Meas. Sci. Technol. 2007, 18, 30–40. [Google Scholar] [CrossRef]
- Li, H.; Feng, S.F. Parameter modulated chaotic communication based on particle fitler. J. Comput. Inform. Syst. 2008, 7, 4417–4424. [Google Scholar]
- Zhang, B.; Chen, M.Y.; Zhou, D.H.; Li, Z.X. Particle-filter-based estimation and prediction of chaotic states. Chaos Solition. Fract. 2007, 32, 1491–1498. [Google Scholar] [CrossRef]
- Grewal, M.S.; Andrews, A.P. Nonlinear filtering. In Kalman Filtering: Theory and Practice Using Matlab, 2nd ed.; Wiley: New York, NY, USA, 2001; pp. 289–314. [Google Scholar]
- Afraimovich, V.; Cordonet, A.; Rulkov, N.F. Generalized synchronization of chaos in noninvertible maps. Phys. Rev. E 2002, 66, e016208. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, T.; Zhao, D.; Huang, Z.; Liu, C.; Su, S.; Zhang, Y. Blind Demodulation of Chaotic Direct Sequence Spread Spectrum Signals Based on Particle Filters. Entropy 2013, 15, 3877-3891. https://doi.org/10.3390/e15093877
Li T, Zhao D, Huang Z, Liu C, Su S, Zhang Y. Blind Demodulation of Chaotic Direct Sequence Spread Spectrum Signals Based on Particle Filters. Entropy. 2013; 15(9):3877-3891. https://doi.org/10.3390/e15093877
Chicago/Turabian StyleLi, Ting, Dexin Zhao, Zhiping Huang, Chunwu Liu, Shaojing Su, and Yimeng Zhang. 2013. "Blind Demodulation of Chaotic Direct Sequence Spread Spectrum Signals Based on Particle Filters" Entropy 15, no. 9: 3877-3891. https://doi.org/10.3390/e15093877




