1. Introduction
The way in which deformation is considered from a thermodynamic point of view depends largely on the kind of systems and processes in which one is interested. People engaged in applied continuum mechanics, as well as in engineering geology or geotechnical engineering and dealing with short time processes may prefer to consider deformation in the framework of classical (equilibrium) thermodynamics considering a non-hydrostatic state of stress as a state quantity (see, for instance [
1]). Structural geologists, who have a special interest in the modification of rock structure resulting from long-term deformational processes, have good reasons for wanting to use irreversible thermodynamics. For structural geologists, it is not an important loss of information that changes of lengths and/or angles during natural rock deformation cannot normally be measured. To make their retrodictions, that is, to infer explanations or interpretations of past events from the laws that are assumed to have governed them, they are interested in the preserved observable structures and mineral assemblages representing a record of the deformational episodes and displacements of deforming systems within the Earth’s crust.
In the following, closed thermodynamic systems, such as rock bodies consisting in polycrystalline aggregates, will be taken into account. They may undergo an isothermal deformation consisting in a pure volume change or involving shape change. The deformation may result partially from structural modifications, such as those involved in chemical and phase change, that contribute in making a portion of the undergone increment of internal energy unrecoverable as mechanical (elastic) energy. In the case of pure volume change, the identification of the
scalar driving force responsible for a chemical reaction or a phase change does not cause problems. In contrast, an intricate dispute is still open, involving also non-geologists and lasting for one hundred and fifty years, to justify the occurrence of chemical reactions and phase changes during a homogeneous deformation involving the shape change of actual materials. A comprehensive list of papers published in the first century on this subject [
2] and a less exhaustive review of the following literature [
3] are available.
To find a way out of the labyrinth of proposed solutions, a radical reassessment of the approach to the problem of relating deformation with thermodynamics is presented here. It will start with a completion of the definition of Cauchy strain and stress tensors that seems to go far beyond what may ordinarily concern petrologists and structural geologists. Then, an ignored, or at least undervalued, property of second rank tensors will be considered to define the kind of information that stress and strain analysis can furnish for the foundation of the thermodynamics of deformable materials. Lastly, it will be shown how the production of entropy in deforming materials could be conceived.
2. A Basis for a General Description of Change of Shape and/or Volume
By definition, a strain tensor describes a geometrical transformation without considering changes of the original isotropy or anisotropy of the real system, that is, a physical system made of a large number of discrete elements (atoms, molecules and crystal grains), represented by the deforming continuum. In other words, an isotropic continuum playing the role of a statistically isotropic actual material is thought of as preserving its original isotropy during deformation. In reality, a closed thermodynamic system consisting in a volume element of a deformable actual material, whose structure is statistically isotropic in the undeformed state, preserves its original shape together with its original isotropy only if its deformation consists in volume change not involving shape change. It loses its isotropy when undergoing shape change. Streaming birefringence shows that even liquids that are (statistically) isotropic at rest lose their isotropy when they flow.
Among the homogeneous deformations involving shape change, it is possible to distinguish those characterized by the transformation of a volume element of cubic shape into a rectangular parallelepiped (while its structure becomes either transversely (laterally) isotropic or orthorhombic, with axes and planes of symmetry parallel to the edges and faces of the parallelepiped) and those characterized by the transformation of a cubic element into a non-rectangular parallelepiped (while its structure becomes monoclinic or triclinic). The first kind of deformation will be considered here as irrotational, the second one as rotational.
A continuum system was thought of by Cauchy as a convenient alternative to a discrete one made of material points (atoms or molecules) that may come closer or farther, due to attraction and repulsion forces [
4,
5]. The refinement of the original Cauchy assumption that will be exposed in the following is grounded on the assumption that the modification of the average internuclear distances, and the consequent change in internal energy, results not only from changes of average bond lengths, but also from changes of bond angles (torsional rotational angles included). As a limiting case, which may be accepted only as an approximation within certain conditions for some actual materials, one may consider the ideal elastic behavior. In that case, the assumption that changes of bond angles occur together with those of bond lengths is a way to justify the fact that lengthening may occur in directions of compression and
vice versa. In reality, it must be taken into account that, since the above changes result, to a certain extent, from phenomena, such as the onset of damages in crystals and change of the average size of crystal grains in polycrystals, or phase changes and chemical reactions, part of the increase of internal energy in a deforming body does not consist in elastic energy.
Here, the geometrical transformation of a cubic element of an actual material consisting in pure volume change will be considered as resulting from the modification of the average internuclear distances, which is equal in every direction. On the contrary, for deformations involving shape change, such modification, being not equal in different directions, is responsible for making the original isotropic structure anisotropic. In order to distinguish irrotational and rotational deformations, one may consider that they result from the transformation of the orthonormal vector space, whose mutually perpendicular basis vectors, parallel to the edges of the cubic volume element, have the length, , in the undeformed state. This is transformed into a vector space, whose basis vectors, , and , have the lengths, , and , and form the angles, α, β and γ, which may or may not be equal to .
Assuming that the system is isotropic and that the original volume,
, is the unit volume, in the undeformed state, the metric tensor,
, of the ortho-normal vector space can be considered equal to the Kronecker delta:
A generic homogeneous deformation corresponds to the transformation of the above vector space into a new one, whose metric tensor is:
In irrotational deformations, all the angles, α, β and γ, are equal to , the cross-terms vanish and the vector space is orthogonal. In rotational deformations, at least one of the above angles is not , so that the vector space is non-orthogonal.
The volume,
V, of either the rectangular or the non-rectangular parallelepiped, in which the originally cubic element of unit volume is transformed, is equal to the scalar triple product,
, that is, to the absolute value of the square root of the determinant of the metric tensor:
In general, the volume of the material element after deformation is:
with:
and the
measurable relative volume change (or
dilatation, or
dilation or
expansion) is:
The measurable dilatation due to a generic (either irrotational or rotational) strain may be positive, negative or even null. It is designated here by , since, as it will be shown later, in any deformation involving shape change, the measurable dilatation consists, at any scale, of the algebraic sum of two components to which different thermodynamic meanings must be attributed.
In the particular case of an irrotational deformation,
, so that the measurable dilatation is:
Note that the above formulas are those used in crystallography to calculate the volume of unit cells and distances and angles between atoms in them (see the Online Dictionary of Crystallography: reference.iucr.org/dictionary/Reciprocal space).
3. The Extended, or Generalized, Cauchy Strain Tensor
For irrotational homogeneous deformations, the increments,
,
and
, of the unit length appearing in Equations (6) and (7) can be considered as the principal components of the Cauchy strain tensor, so that the measurable dilatation may be expressed as follows:
where:
are invariant quantities, known as the first, second and third (or linear, quadratic and cubic) invariants of the strain tensor,
.
For generic homogeneous deformation, the measurable dilatation is:
with
.
The above considerations suggest that, in order to represent both irrotational and rotational deformations, one should introduce an extended, or generalized, strain tensor for which the same notation,
, already employed for the components of the Cauchy strain tensor, can be used, merely taking into account that the indices,
i and
j, may refer either to orthogonal or to non-orthogonal Cartesian coordinates. The Cauchy strain tensor,
, may be considered both as an infinitesimal and a finite strain tensor for all deformations that do not involve internal rotation [
6,
7]. It must be pointed out that, also, the extended tensor here defined may be considered both as an infinitesimal and a finite strain tensor.
4. The Two Components of the Measurable Change of Volume
In the debate about the driving force responsible for chemical reactions or phase changes and those accounting for strain anisotropy, there are authors that show some confidence in a particular decomposition of the Cauchy symmetric tensor of infinitesimal strain,
(with the indices,
i and
j, referring only to orthogonal Cartesian coordinates). They decompose the tensor into the sum of a tensor that describes a deformation consisting in a pure
dilatation and a traceless (or trace-free) tensor, currently known as the strain deviator or deviatoric strain tensor, which describes a deformation consisting in pure distortion (that is, in a change of shape not involving volume change). In the fourth edition of its Mathematical Theory of Elasticity, Love introduces this decomposition, calling it ‘resolution’ ([
8]: pages 47 and 83). The decomposition of the strain tensor is associated with that of the state of stress, considered as equal to the sum of two parts, one of which would be responsible for dilatation and the other for distortion (respectively, ‘mean tension’ and ‘shearing stress’, according to Love). Later on, the decomposition of a second rank tensor into irreducible tensorial parts, to which different physical meanings are attributed, was introduced in different physical contexts. It happens that the resort to such a decomposition in quantum mechanics is justified ([
9,
10]: pages 8,18–30, 243; [
11]: pages 10.6–10.10), making reference to that of the case of the infinitesimal strain tensor.
In rheology, still considering infinitesimal strains, this decomposition is used to describe the behavior of ideal bodies that serve as ‘standard of comparison’ for the behavior of actual materials. Two independent rheological equations are considered: the volumetric equation, describing the relation between dilatation and isotropic pressure, and the distortional equation, describing that between the deviators of stress and strain (and their time derivatives).
A decomposition into the sum of a volumetric part and a traceless part not implying volume change cannot be proposed for a finite state of strain. Actually, for finite strains, such a tensor can be decomposed either into the sum of an isotropic part involving the total relative volume change and an anisotropic one, which is not traceless; or in a traceless part and an isotropic one, which involves a relative volume change, which is different from the total one. Moreover, in both cases, the anisotropic part involves volume change, and the sums of the volume changes ensuing from the isotropic and the anisotropic tensors for the two alternatives are different, and neither are equal to the measurable volume change.
In some cases, the behavior of actual materials subjected to large deformations in experimental tests fails to meet the expectations grounded on the above premises, so that often, it was necessary to resort to exceptional explanations. The question is whether such empirically recognized failures arise because of the improper extension to large deformations of rules that can be considered only approximately valid for small deformations.
In order to consider relations between stress and strain, small irrotational deformations are currently taken into account, disregarding the second and third invariants of the symmetric stress and strain tensors. Unfortunately, what was discarded in the description of a small event cannot miraculously reappear in the description of a chain of many small events. Clearly, the assumption that large deformations can be considered as a sequence of small deformations is questionable.
It will be shown that considering homogeneous finite strains first, and then infinitesimal strains as a limiting case, is more rewarding. The proposed approach leads to the identification of a different, unique, decomposition of both the classical and the extended form of the strain tensor (and of the corresponding stress tensor describing the internal reaction to the forces acting on the deforming body). The recognition of this decomposition turns out to be indispensable in order to include deformations involving shape change among the physical processes simultaneously taking place in thermodynamic transformations.
In the following, first, only irrotational deformations of a volume element, which can be described by a symmetric second rank strain tensor, will be taken into account. The same symbol, ε, will be employed for the components of both infinitesimal and finite strain tensors.
5. The Dilatation Components in a Homogeneous Irrotational Deformation
In general, an irrotational deformation described by the symmetric strain tensor,
, involves the measurable dilatation, which is expressed by Equation (8). It is currently accepted that the assumption that, dealing with
infinitesimal strains, one is allowed to regard as negligible the quadratic and cubic invariants,
and
(that is, to regard them as equal to zero), and to consider the dilatation equal to the linear invariant,
. This assumption is considered convenient, because it allows the decomposition of the infinitesimal strain tensor into the sum of a ‘volumetric’ part:
where:
is an invariant scalar quantity and
is the Kronecker delta; and a traceless ‘deviatoric’ part:
that does not involve any change of volume.
Even if the zeroing of the far small terms of a sum can be seen as a licit approximation, the above assumption is questionable, because it leads to two conflicting ways of conceiving the decomposition of finite and infinitesimal strains. The conflict becomes evident when one considers the decomposition of an infinitesimal state of strain as a limit case of that of a finite state of strain.
First of all, it must be noted that the above mentioned ’classical’ decomposition of the infinitesimal strain tensor in a volumetric and a deviatoric traceless part turns out to be one of the infinite possible decompositions of the symmetric infinitesimal strain tensor, , into the algebraic sum of a non-spherical part, , and a spherical one, , such that the sum of the dilatations involved by the latter ones is equal to the dilatation involved by the former. In contrast, for finite strains only one decomposition exists for which the sum of the dilatations involved by the non-spherical part, , and the spherical one, , is equal to the dilatation involved by the tensor, .
The value,
G, of the principal components of the spherical tensor,
, satisfying the above condition is obtained solving the following equation:
where:
, and are, respectively, the first, second and third invariant of the tensor, ;
, and are the first, second and third invariant of its anisotropic part, ;
, and are the first, second and third invariant of its isotropic part, .
Equation (16) turns out to be a first degree equation that can be rewritten as follows:
If the principal components,
,
and
, of the tensor,
, are known, the value,
G, of the components of the spherical part can be obtained solving Equation (17). One finds that
G is a function of the linear and quadratic invariants,
and
, of the tensor,
, and is independent from the value of the cubic invariant,
The spherical (isotropic) and the non-spherical (anisotropic) parts of the strain tensor are:
and:
Once knowing the value of
G, one may consider the measurable dilatation,
, as equal to the algebraic sum of the ‘isotropic dilatation’ (more properly, ‘the dilatation involved by the isotropic part of the strain tensor’):
and the ‘anisotropic dilatation’ (more properly, ‘the dilatation involved by the anisotropic part of the strain tensor’):
It must be noted that, while the isotropic dilatation may consist either in a volume increase or a volume decrease, the anisotropic dilatation has always the same sign: the one assigned to volume decrease.
A state of strain
1-does not involve anisotropic dilatation if:
2-does not involve isotropic dilatation if
, that is, if:
3-is isochoric (isovolumetric) if the isotropic dilatation consists in a relative volume increase having the same absolute value of the anisotropic volume decrease.
4-must involve at least one of the two contributions to the relative volume change different from zero, because Conditions 1 and 2 can be satisfied together only if .
A number of incongruences result from the assumption that
has to be considered equal to zero for infinitesimal strains. For instance:
One must conclude that the same expressions used to deal with finite strains must be used also to deal with infinitesimal strains. After all, since it is likely that different physical meanings should be attributed to the two contributions to the relative volume change, the distinction of them must be possible both for finite and infinitesimal strains. It is likely that physical processes that alone would preserve the original symmetry of a statistically isotropic system made of a large number of discrete elements (atoms, molecules and crystal grains) should be related with the isotropic dilatation; production of structural anisotropy with the anisotropic dilatation. In a polycrystalline aggregate, chemical reactions, phase transformations and mass transfer leading to changes of the average grain size are examples of the first kind of processes; mass transfer leading to preferred orientation of crystal lattices and/or of grain boundaries is an example of the second kind of processes. Therefore, the two components of dilatation are associable with distinct contributions to the change in internal energy of the deformed material system and/or to the production of entropy during deformation.
6. The Two Components of Volume Change in Rotational Deformations
It can be shown that the distinction of the two components is possible for any kind of homogeneous deformation: that is, also for rotational deformations.
Two limit cases, will be considered here.
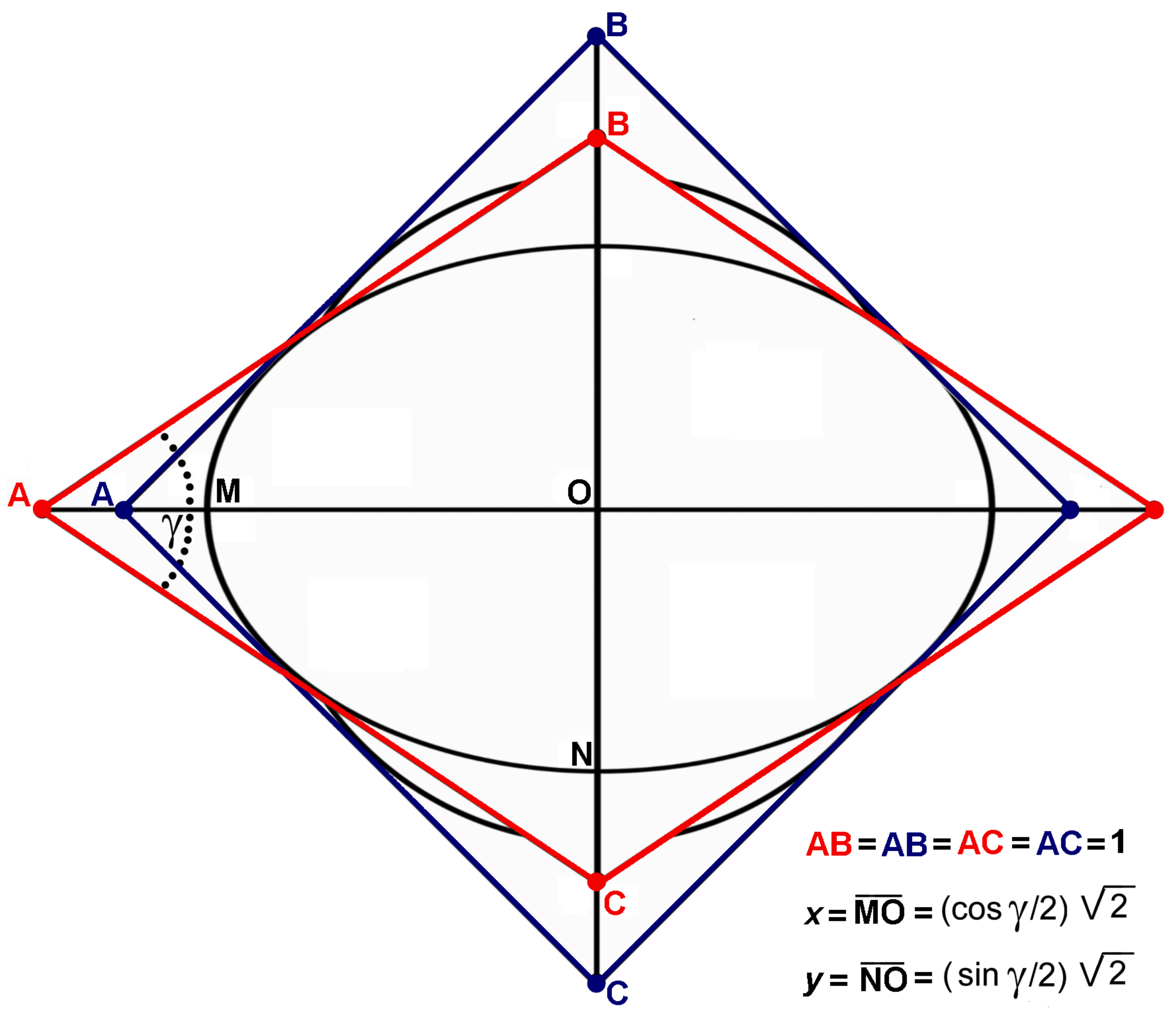
In an irrotational deformation of the type considered in the previous section, universally known as
pure shear strain, the metric tensor of the vector space (1) is transformed into the metric tensor:
in a deformation-that could be called
strain by internal rotation in which the length of the basis vectors remain unchanged, while the angles that they form change, the metric tensor of the vector space (1) is transformed into the metric tensor:
The directions of the axes of the deformation ellipsoid coincide with those of the basis vectors in pure shear strain; they do not coincide with them in strain by internal rotation (actually, they bisect the angles formed by the basis vectors). Therefore, the lengths of the axes are independent from each other in pure shear strain; they are not independent in strain by internal rotation. For example, if only one of the angles between the basis vectors, for instance,
γ, is smaller than
, while the length of all the basis vectors remains unchanged, the metric tensor of the vector space (1) is transformed into the metric tensor:
In this case, the maximum semiaxis of the deformation ellipsoid, whose direction bisects the angle,
γ, is:
and the minimum semiaxis of the deformation ellipsoid, whose direction bisects the angle,
, is:
so that:
In a section parallel to the plane,
, the above strain is perfectly represented by the
trellis model (
Figure 1) that was suggested as a simulation of the deformational behavior of woven fabrics under a simple pull [
12,
13].
Figure 1.
The model introduced by Weissemberg consists of four rigid rods of unit length that are pin-pivoted at their end as a trellis. After deformation, the four pivots located at the corners of the blue square reach the corners of the red parallelogram. This model is considered here as a graphical representation of a plane strain by internal rotation, due to a system of counteracting couples.
Figure 1.
The model introduced by Weissemberg consists of four rigid rods of unit length that are pin-pivoted at their end as a trellis. After deformation, the four pivots located at the corners of the blue square reach the corners of the red parallelogram. This model is considered here as a graphical representation of a plane strain by internal rotation, due to a system of counteracting couples.
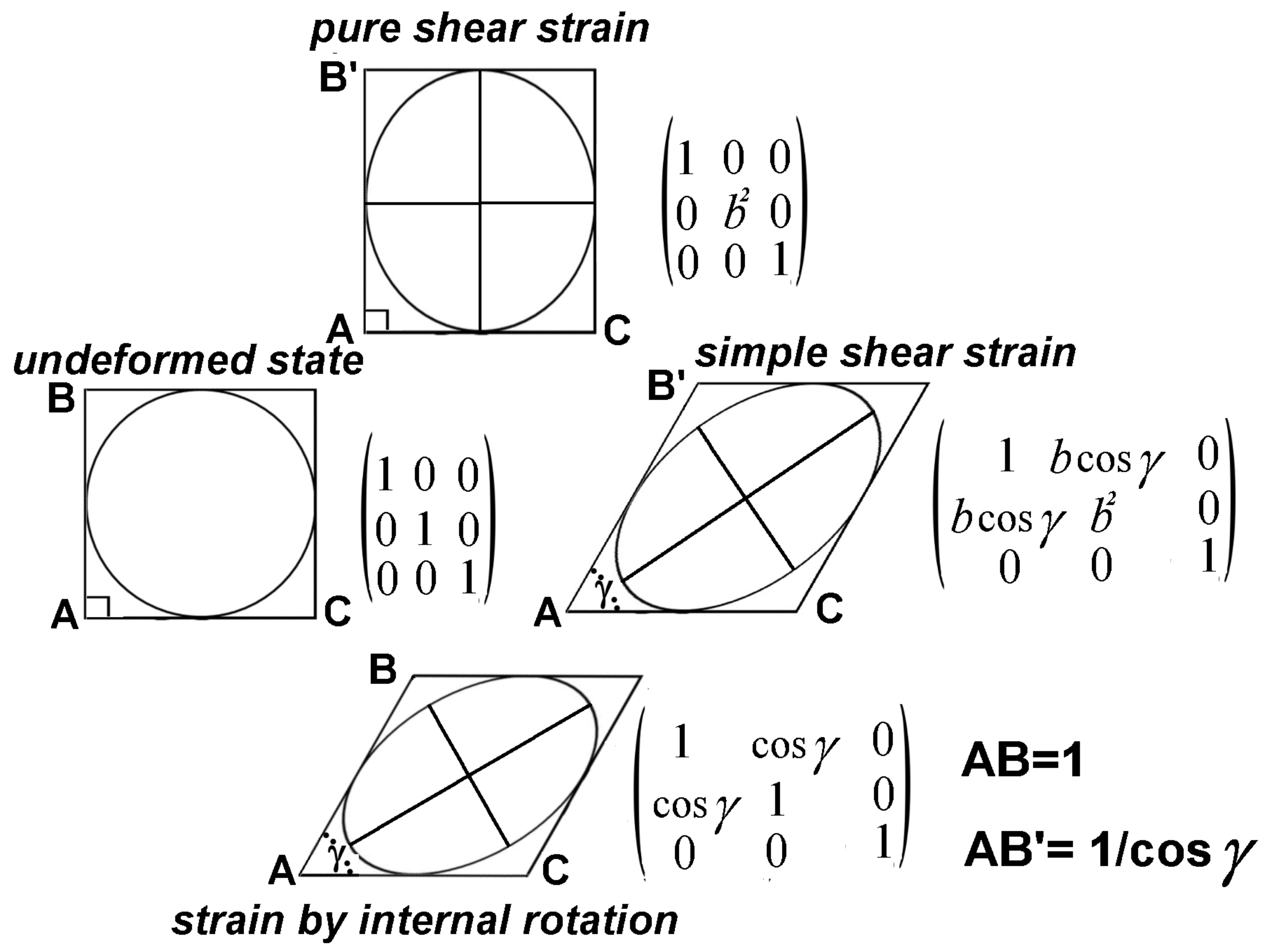
A generic rotational deformation may result from simultaneous concurrence of pure shear strain and strain by internal rotation, or from a sequence of any one of these kinds of deformation followed by the other one. The case of simple shear, which is a case of rotational deformation and not a limit case, is represented in
Figure 2.
Figure 2.
Simple shear strain seen as rotational strain resulting from strain by internal rotation followed by pure strain or by pure strain followed by strain by internal rotation or by a combination of both of them.
Figure 2.
Simple shear strain seen as rotational strain resulting from strain by internal rotation followed by pure strain or by pure strain followed by strain by internal rotation or by a combination of both of them.
7. Internal Reactions to the External Actions within a Homogeneous Volume Element of the Earth’s Crust
In principle, a structural geologist is inclined to assume that a volume element of the Earth’s crust, small enough to make the gravity gradient negligible and considered as a closed thermodynamic system, to be in thermodynamic equilibrium at a certain temperature, should be statistically homogeneous (in composition and structure), statistically isotropic and subjected to a hydrostatic pressure, (often called lithostatic in this context).
It seems reasonable to assume that the components of the internal reaction to the external forces responsible for the deformation are related with the modification of the internuclear distances-resulting from changes of bond lengths and bond angles (torsional rotational angles included)-and then with the components of strain. As shown in
section 2, the deformation of a small-enough homogeneous portion of the Earth’s crust can be represented as the transformation of an orthonormal vector space into a non-orthogonal (or into an orthogonal) vector space. In a state of equilibrium, the moduli of the mutually perpendicular basis vectors, parallel to the edges of a cubic volume element, are proportional to the purely normal compression,
, acting in every direction, and the vector space is characterized by the metric tensor:
Since the compression, , acts equally in every direction, its value can be considered equal to that of a scalar quantity: the equilibrium hydrostatic pressure, , to which the volume, , of the matter making up the system corresponds in a state of equilibrium at a given temperature.
During an isothermal deformation, this vector space is transformed into a new one, whose basis vectors, , and , have the moduli, , and , and form the angles, α, β and γ.
The forced modification of the average internuclear distances during a generic isothermal deformation would involve the transformation of the above orthogonal vector space into a new one, whose metric tensor is:
In irrotational deformations, all the angles, α, β and γ, are equal to , the cross-terms vanish and the vector space is orthogonal. In rotational deformations, at least one of the above angles is different from , so that the vector space is non-orthogonal.
Since the basis vectors of the vector space with the metric tensors (2) and (33) have the same directions, the metric tensor:
is analogous to the vector space with the metric tensor (27).
However, this does not mean that the components of strain by internal rotation correspond to the components of internal reactions counterbalancing couples acting on the deforming volume element.
Taking into account the above considerations, another tensor could be introduced to describe the reactions to the external forces. As well as the denomination stress tensor, the same notation, , could be employed for it, provided that it is taken into account that (a) the indices, i and j, may refer either to orthogonal or non-orthogonal Cartesian coordinates and that (b) the equilibrium pressure is not considered as equal to zero. The above definition of the stress tensor turns out to be beneficial also for both geologists and non-geologists, since it (a) makes possible the definition of the state of stress at a point also in a body on which counterbalanced couples are acting; and (b) is essential for a correct definition of the hydrostatic pressure of which the chemical potentials in a deforming material system are function.
The state of stress existing in an irrotationally deforming material that was originally in equilibrium under the hydrostatic pressure,
, is described by a second rank symmetric tensor,
, that, as any second rank tensor, can be decomposed in a single way into the sum of an isotropic and an anisotropic component:
The isotropic component is:
with:
where
and
are the first and second invariants of the tensor,
.
The hydrostatic pressure,
p, involved by the tensor,
, is a function of its first invariant,
. More precisely, it is equal to a third of it:
The pressure,
, involved by the anisotropic part is:
Note that both the invariants, p and , are scalar quantities with the dimensions, , of a pressure.
It can be shown that the decomposition of the stress tensor into the algebraic sum of an isotropic part and an anisotropic one can be performed also for the states of stress corresponding to rotational deformation.
8. Entropy Production in Material Systems Undergoing Deformation
A natural extension of thermodynamics to actual systems (made of a large number of discrete elements, such as atoms, molecules and crystal grains) away from, but close to, equilibrium, is based on the local equilibrium hypothesis, that is, on the assumption that these systems can be viewed as formed of homogeneous subsystems, where the rules of equilibrium thermodynamics apply. Since empirical evidence shows that strain anisotropy spontaneously tends to disappear, the use of the local equilibrium hypothesis should be considered unacceptable for homogeneous sub-systems that undergo deformation involving production of strain anisotropy, since they, being anisotropic, are intrinsically out of equilibrium. In spite of this, it is assumed here that for homogeneous subsystems, production of entropy can be defined provided that it is considered as consisting of two different contributions, respectively related to the isotropic and anisotropic volume change. It is the recognition and interpretation of the two components of volume increment, or specific volume increment (not of dilatation, that is, of adimensional relative volume change) and of the two corresponding components of pressure inferred from the consideration of the strain and stress tensors, as they are defined above, that allows the acknowledgment of deformation as one of the physical processes taking place in thermodynamic transformations.
The changes in entropy in a closed system can be expressed as a sum of two parts:
where
is the entropy change due to exchange of energy with the exterior and
is the entropy produced by the irreversible processes in the interior of the system. In a deformational process, the first one takes place until work is done on the system; the second starts as soon as the system is brought out of equilibrium and continues even if the system becomes isolated at constant volume.
If the deformation consists in a pure volume change, the entropy increment expressed in terms of exchange of heat with the exterior is (see [
14] : pages 87–88):
where:
is the amount of heat exchanged by the system in a time, ,
p is what is known as the hydrostatic pressure associated with the recoverable volume change, .
is the increment of potential energy non-recoverable as mechanical (elastic) energy, resulting from irreversible processes, including chemical reactions and phase transformations, which are responsible for part of the volume change and leave the original statistical isotropy unchanged.
For deformations involving shape change, a further term must be considered:
where:
is the quantity introduced in Equation (22),
is the quantity of Equation (40),
is the increment of potential energy involving volume change due to processes responsible for the production of anisotropy
and , is the Gibbs’ capacity for entropy.
The quantities marked by the tilde are process quantities, that is, quantities that characterize the transition of the system from an equilibrium state to another equilibrium state. Isolating the deforming body and maintaining it at constant volume, the spontaneous production (increase) of entropy would continue until the departure from equilibrium disappears with the zeroing of these quantities.
It must be noted that the Gibbs’ definition of the capacity for entropy [
15], that is
“the amount by which the entropy of the body can be increased without changing the energy of the body or increasing its volume”
corresponds to the definition of
negentropy used in information theory.
The exchange of energy with the exterior that brings a deformable system out of equilibrium, together with the spontaneous processes (actually triggered by the departure from equilibrium) tending to re-establish an equilibrium state results in variations of the values of the scalar variables, , , and . The mechanical behavior of a given material at constant temperature depends on the rate of these changes and from the change of these rates with time, which may be very different for every single variable.
The formulation of Equations (42) and (43) was made without taking into account constitutive assumptions. However, the variables, and , representing increments of energy recoverable as mechanical energy, are clearly related with what is known as elastic behavior; the variables, and , with the inelastic (non-elastic) behavior. In deformations that are slow enough to maintain the system not far from equilibrium, the crossing of critical thresholds may be avoided. In this case, the inelastic component makes one think of the behavior known as viscous. For small deformations, the whole behavior could be considered as linearly viscoelastic. Note, however, that the linearity considered here consists in the proportionality between invariant scalar quantities and not between components of tensors.
9. Discussion
In the literature dealing with irreversible thermodynamics, the resort to symmetry arguments is recurrent. With a variable degree of confidence in them (from firm trust, to total dissent), many authors make reference to the Curie’s statements—considered as either a single or three symmetry principles—about symmetry in physical phenomena ([
16]; English translation by the authors in [
17]),
“The characteristic symmetry of a phenomenon is the maximum compatible with the existence of the phenomenon. A phenomenon can exist in a medium that possesses its characteristic symmetry or that of one of the subgroups of its characteristic symmetry. In other words, certain elements of symmetry can coexist with certain phenomena but they are not necessary. What is necessary is that certain elements of symmetry do not exist. It is the dissymmetry that creates the phenomenon.”
“When several phenomena of different nature are superposed in the same system, the dissymmetries are added. Therefore, there only remain as symmetry elements in the system those which are common to each phenomenon taken separately.”
“When certain causes produce certain effects, the symmetry elements of the causes must be found again in the effects produced. When certain effects show a certain dissymmetry, this dissymmetry must also be found in the causes that have given rise to them. The converse of these two propositions is not true, at least in practice: that is to say, the effects produced can be more symmetrical than the causes.”
It happens that some authors, supposedly inspired by Curie’s statements, maintain that all ‘coupling’ between quantities of different tensorial character are forbidden [
18,
19,
20], while Truesdell [
21] set off a scathing attack on who believes such a rule. Curiously, through the introduction of a
tensorial chemical potential as the driving force for a chemical and/or phase change in a solid under non-hydrostatic state of stress, the same author [
21,
22] ends up finding a way to comply with the rule he is rejecting. In the geological literature, the above assumption has been accepted by some authors [
23,
24,
25], while another one introduces the questionable concept of the scalar
non-equilibrium chemical potential of each component of a deforming body, considered as a function of the scalar product of stress and strain deviators [
26].
Actually, there should be no reason to extend the above contrast to the case of production of chemical reactions and/or phase transformations (a scalar ‘effect’) in a body subjected to a non-hydrostatic state of stress. As a matter of fact, in the last statement, Curie makes reference to an exception that could include this case. Actually, Curie, who uses the expression ‘a certain dissymmetry’ with the meaning of ‘lack of certain elements of symmetry’, seems inclined to consider this exception as a problem of perception. Just after the above statement, he says that minor effects, being too weak to be discerned, amount to the same as no effects in practice ([
16]: page 127).
The thesis maintained here is that one should neither resort to Curie’s conjecture above, nor to the consideration of a
tensorial chemical potential, since a more convincing idea is to conform with the Curie’s symmetry principle(s) devoid of exceptions: namely, the idea, shared by a large audience, that a second rank symmetric tensor can be decomposed into the sum of parts with different symmetries and then with different physical meanings. In the present article, an original way is suggested to decompose the tensors of strain and stress into the sum of two parts, one of which is isotropic. The proposed interpretation of the different physical meanings of the two parts is supported by empirical evidence. The volume variation due to chemical reactions, phase changes and other phenomena, such as the change of the average size of crystal grains in a polycrystal, is easily perceived. Moreover, it is experimentally proven that the production of anisotropy during deformation involves increase of bulk density (see, for instance, [
27,
28]) and that the spontaneous reduction of strain anisotropy, artificially enhanced by heating the deformed object, involves the opposite density change (see, for instance, [
29]).
The priority given to the description of finite strains highlights something else that cannot be detectable in the description of infinitesimal strains. Dealing with closed systems undergoing isothermal deformation, one is allowed to choose as original unit volume the
specific volume,
, in the undeformed state at the given temperature, instead of an arbitrary volume,
. It turns out that the metric tensor of the reciprocal vector space is
and the triple product of the reciprocal basis vectors:
is:
where Φ is the quantity (5),
v is the specific volume and
ρ is the bulk density of the matter of which the system is made. Therefore, it becomes clear that the conservation of the volume change in the suggested decomposition of the strain tensor implies the conservation of mass: a prerequisite for considering the phenomenon of deformation in non-relativistic thermodynamics.
The length of the reciprocal basis vectors can be considered as a function of the linear mass density (measure of mass per unit length) along their directions. At a given instant, the strain anisotropy results from the relative displacements undergone by the atoms making up the body, which to a certain extent, are a function of the system of forces acting on it. Consequently, the instantaneous internal reaction counterbalancing the external actions, that is, the state of stress, is intrinsically a function of the state of strain. Inasmuch, the definition of the state of strain suggested here may describe also rotational deformations: the state of stress corresponding to a given state of strain takes into account also the internal reactions counterbalancing the couples acting on the deforming body.
The fact, that it is impossible to perform experiments in which homogeneous deformation of a whole sample is obtained shows that strain anisotropy may appear only in systems undergoing inhomogeneous deformation. Therefore, only what occurs in a homogeneous portion of a deforming system can be described, provided that it is assumed that the homogeneity is preserved throughout the deformational process. The
state variables to be considered to define the instantaneous equilibrium state of a given assemblage of minerals in a deforming rock are the same that are used to describe the equilibrium state of a gas; the definition of the simultaneous departure from the disorder characterizing equilibrium requires the consideration of the
process variables defined in
Section 8.
When work is done on the deforming system from the exterior, the progressive increase of capacity for entropy involves a progressive increase of Gibbs’ free energy. In metallurgy, such ‘storage’ of energy has been recognized and experimentally measured, starting from the thirties of the twentieth century [
30,
31,
32]. Presently, it is widely recognized that the anisotropic structure of cold-worked metals is ‘unstable’ and that ‘under favorable circumstances’ (that is, enhancing the mobility of the atoms by heating the deformed body), cold-worked metals ‘undergo the processes of recovery and recrystallization’ (that is, processes tending to reduce the strain anisotropy), releasing the ‘stored energy’ in the form of heat (see [
33]; page 147). Even if most of the work done on deforming metals is transformed in heat and a very small amount remains as stored energy (see, for instance [
34]), the latter phenomenon is responsible for changes of properties that are relevant for the use and/or processing of these materials. Therefore, one may understand why metallurgist do not focus principally on the above spontaneous tendency towards isotropy, which is only one of the many changes in which they are interested (see, for instance [
35]). Actually, from a thermodynamic point of view, such spontaneous tendency towards disorder should deserve the main attention, since it parallels the behavior of condensed matter with that of gases. An analogous behavior is shown by materials other than metals. Geologists recognize the evidence of recovery and recrystallization in naturally deformed rocks.
Summing up, relaxation in a deformed solid does not consist only in stress relaxation.
To conclude, we need to go back to the leitmotiv of the present paper, namely, to the problem of defining the driving forces responsible for chemical reactions and phase changes in a system undergoing a deformation involving shape change. In such a system, the hypothesis of local equilibrium should not be made in general. However, for phenomena that are merely a function of state variables, such as chemical reactions and phase changes, the resort to this hypothesis is still admissible. On the contrary, the assumption of a dependence of these phenomena from the path-dependent values of process variables would make undefinable the driving force responsible for them.
The resort to symmetry arguments is one of the main resources a structural geologist has to obtain information on the past events in which he is concerned. This particular interest is documented in a well-known article on the use of symmetry concepts in the structural analysis of deformed rocks [
17]. The first part of this article, devoted to the symmetry of physical phenomena, is a flawless masterpiece. In the second part, dealing with applications, one may find some questionable interpretations that, according to the writer of the present article, are all imputable to some inadequacy of the available theoretical treatment of deformation. Hopefully, the approach suggested here could be a starting point to improve the geologist’s ability in making his retrodictions; on the condition that it will be shared with non geologists!
10. Appendix: The ‘Rubber Band’
Natural rubber is the forerunner of a very important class of strategic materials: the elastomers. It shows a behavior that at first was considered as the opposite of the “expected” one [
36,
37]. For instance, when stretched, it becomes warmer; it cools if, after having been allowed to come to equilibrium in the stretched state, the tension is progressively released. This phenomenon is related with the so-called Gough-Joule effect, consisting in the length decrease of a rubber band extended by a suspended weight when it is heated. Following the first enunciation by Meyer and Ferri [
38], it is currently assumed that the elastic behavior of rubber does not arise from the forces between molecules, but from the thermal energy of the atoms making up the long-chain molecules. The idea is widely accepted that its deformation involves reduction of entropy rather than an increase of internal energy, as occurs in “ordinary” solids [
39,
40,
41]. Consequently, expressions, such as ‘the rubber elasticity is entropic’, ‘the elastic force is entropy induced’, or ‘energy plays no role in rubber elasticity’, are commonly in use.
The introduction of the concept of ‘entropic elasticity’, peculiar of elastomers, in contrast with that of ‘energetic elasticity’, characterizing other materials, is in line with the persistent tendency to compartmentalize materials in classes. Even though this procedure is of undeniable practical convenience, looking ahead, the search for general rules that may clarify the interrelations between disparate phenomena in disparate materials should not be left aside. That is why, in order to make some important generalizations, an unusual approach to the thermodynamics of deforming materials is proposed in the present paper. The correctness, or at least, the convenience, of the suggested approach seems to be supported by the easy way in which some otherwise puzzling phenomena, such as the observable isochoric elastic deformation of some materials, could be explained in full compliance with rules that are valid for any solid.
A solid material can undergo isochoric deformation in tests involving change of shape while its volume changes in response to a variation of hydrostatic pressure. The arguments exposed in the article lead to believe that in the former case, the lack of measurable volume change results from the fact that the isotropic and anisotropic parts of dilatation and (that is, the volume changes involved by the isotropic and the anisotropic part of the strain tensor, as are defined in section 7) have in the performed tests (more or less approximately) the same absolute value and opposite sign. During the stretching of the rubber band, the isotropic volume change consists (due to the modality of the test) in volume increase and the anisotropic one (as usually) in volume decrease; during the reduction of the tension, the isotropic volume change would consist in volume decrease and the anisotropic volume change in volume increase. During the stretching, the production of entropy (entropy increase) associated with the isotropic volume increase, initially prevails over the production of negentropy (entropy decrease) due to the anisotropic volume change (that is, to the anisotropization of the rubber structure). It becomes smaller than the latter after the crossing of the so-called thermoelastic inversion point. It is likely that this behavior depends on the way in which the values of the isotropic and anisotropic components of pressure p and , and of volume and , change with the progress of the deformation. During the rubber stretching, would be initially higher than ; after the inversion point the latter would become higher that the former. Production of entropy (entropy increase) prevails over production of negentropy (entropy decrease) due to the anisotropization before the inversion point; the opposite occurs during the reduction of the tension.
In contrast, in the far limited range of elastic behavior of other materials, such as metals or rocks, the above inversion simply does not occur.
As observed by Callen (see [
42], page 80), among the quantities of macroscopic interest taken into account when dealing with rubber elasticity, there are the length,
L, of the rubber specimen, that
for a stretched rubber specimen plays the role of the volume, and the tension, that plays the role of the pressure. In contrast, what is proposed here is that
for a stretched specimen of any solid material (rubber included), instead of the change of length and of the tension, respectively, the two components of the volume and the two components of the pressure must be taken into account.
A further generalization may be suggested: namely, that, in order to relate deformation and thermodynamics, for any kind of homogeneous deformation of any kind of condensed matter, the two contributions to both volume change and pressure should be taken into account. The volume elasticity of a gas (and that of a solid in response to a variation of hydrostatic pressure) should be considered just as a limit case: the one in which the anisotropic contribution to the pressure is equal to zero.
The introduction to the fifth chapter of a book by Mueller and Weiss [
43] ends with the comment on a hypothetical joker of the similarity attributed to the behaviors of rubber and gases; ‘rubbers are the ideal gases among the solids’. It is evident that the comparison between rubber and gases to which the authors make reference is quite different from the one between rubber and non-rubber-like solids that is suggested here. Atoms or molecules of a large enough volume element of a solid in an equilibrium state, as the atoms or molecules of a large enough volume element of a gas in thermodynamic equilibrium, move with equal probability in every direction at the same average speed. In general, atoms making up solids can oscillate around a certain location that, in turn, can move to a certain extent with respect to locations pertaining to other atoms. In addition, as for a gas, for a solid, the equilibrium condition implies; that the average distances between atoms or molecules is equal in any direction, that is, that the medium is statistically isotropic (a condition that, in turn, implies that it must be subjected to hydrostatic pressure).
Obviously, there is a relationship between the departure from randomness of motions and the concomitant local departure from uniformity of the average distance between atoms in different directions that may occur in solids (and, in general, in condensed matter).
In principle, one could envisage two different approaches, assuming that (a) the mechanical behavior of deformable solids arises from the forces between molecules or, alternatively, that (b) it depends on the movement of the atoms making up molecules and/or crystal grains. The first approach is the well tested one of the classical rheology, consisting in the definition of suitable constitutive equations in which the components of tensorial quantities, such as the ones describing states of stress and strain and their variation with time, have the right to appear; the second, such as the one proposed here, in which only invariant quantities involved by the same tensors may be taken into account. The two approaches are both useful, because of their complementarity. However, one should expect that their integration could not be obtained through the hybrid expressions that are cultivated today.
The considerations exposed in the present article have been motivated by the search for a suitable definition of the hydrostatic pressure of which phase changes and chemical reactions taking place during rock metamorphism are a function. The decision of submitting them to a broader audience is a consequence of the fact that the conclusions reached are far more intriguing than expected; worthy of a larger diffusion.