Size Effects on the Entropy Production in Oscillatory Flow between Parallel Plates
Abstract
:1. Introduction
2. Transport Problem
2.1. Basic Assumptions
2.2. Fundamental Equations
2.3. Velocity Field
2.4. Temperature Field
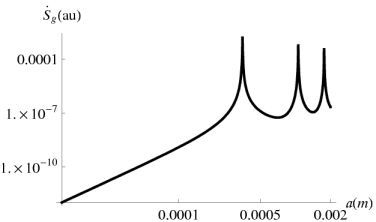
3. Results and Discussion
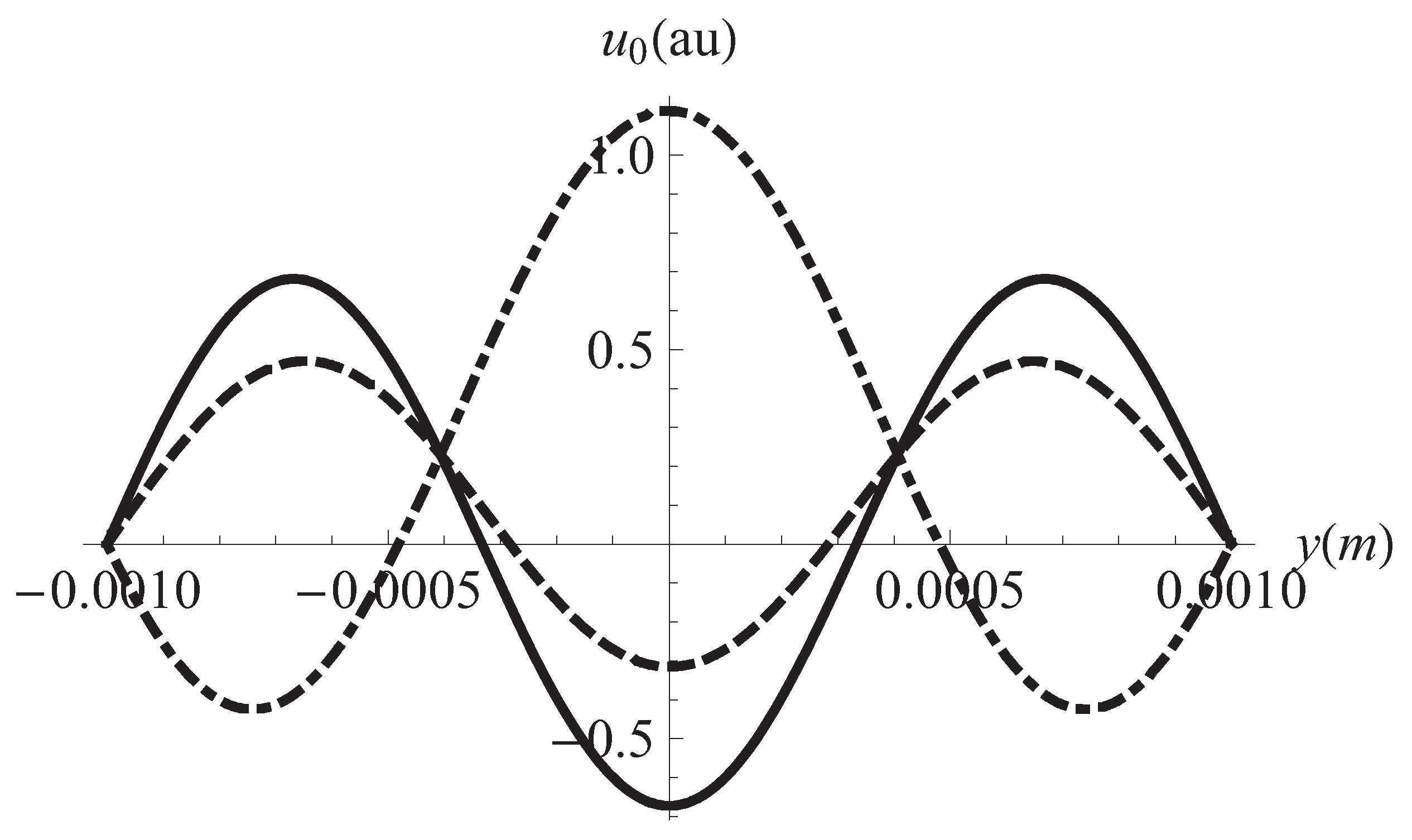
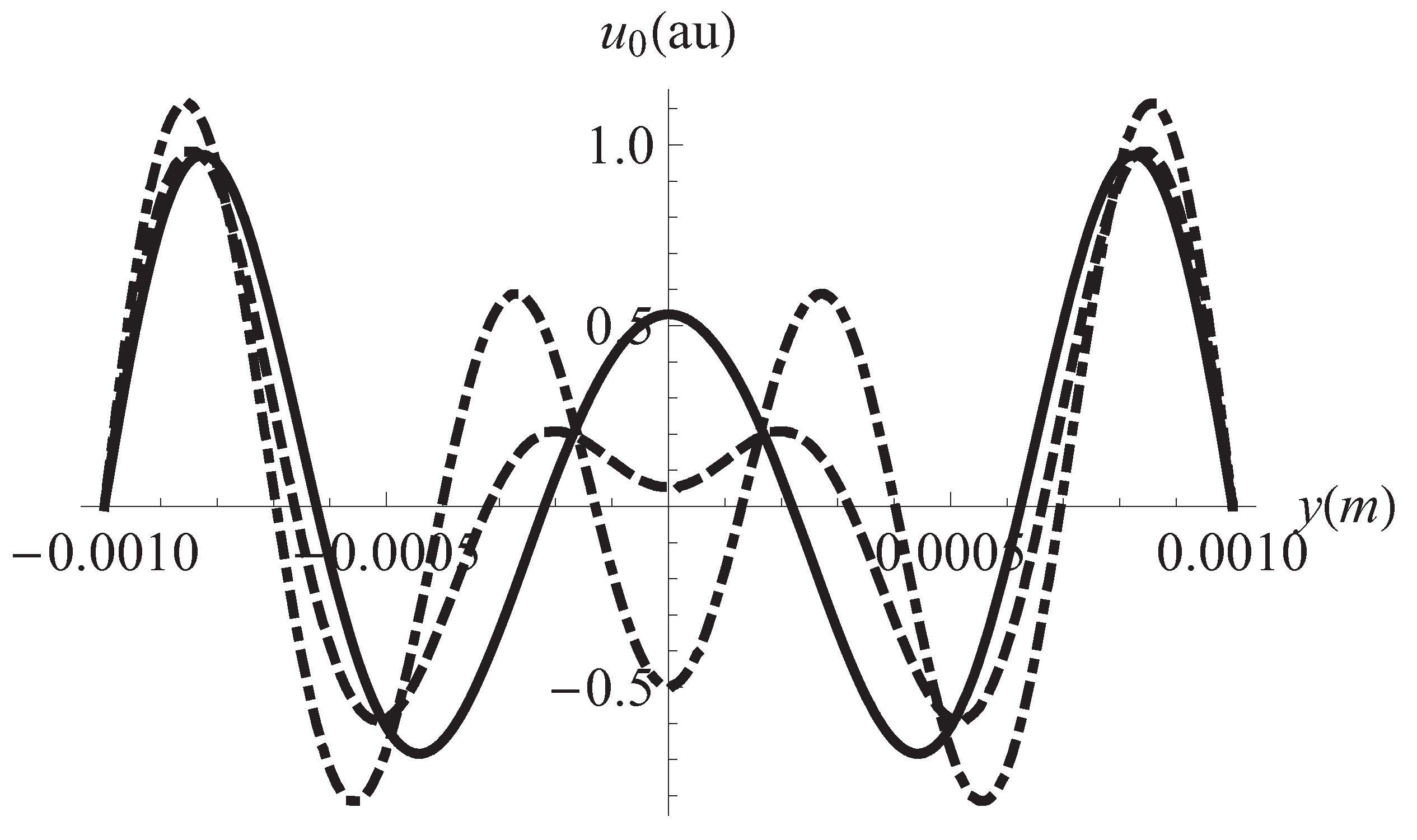

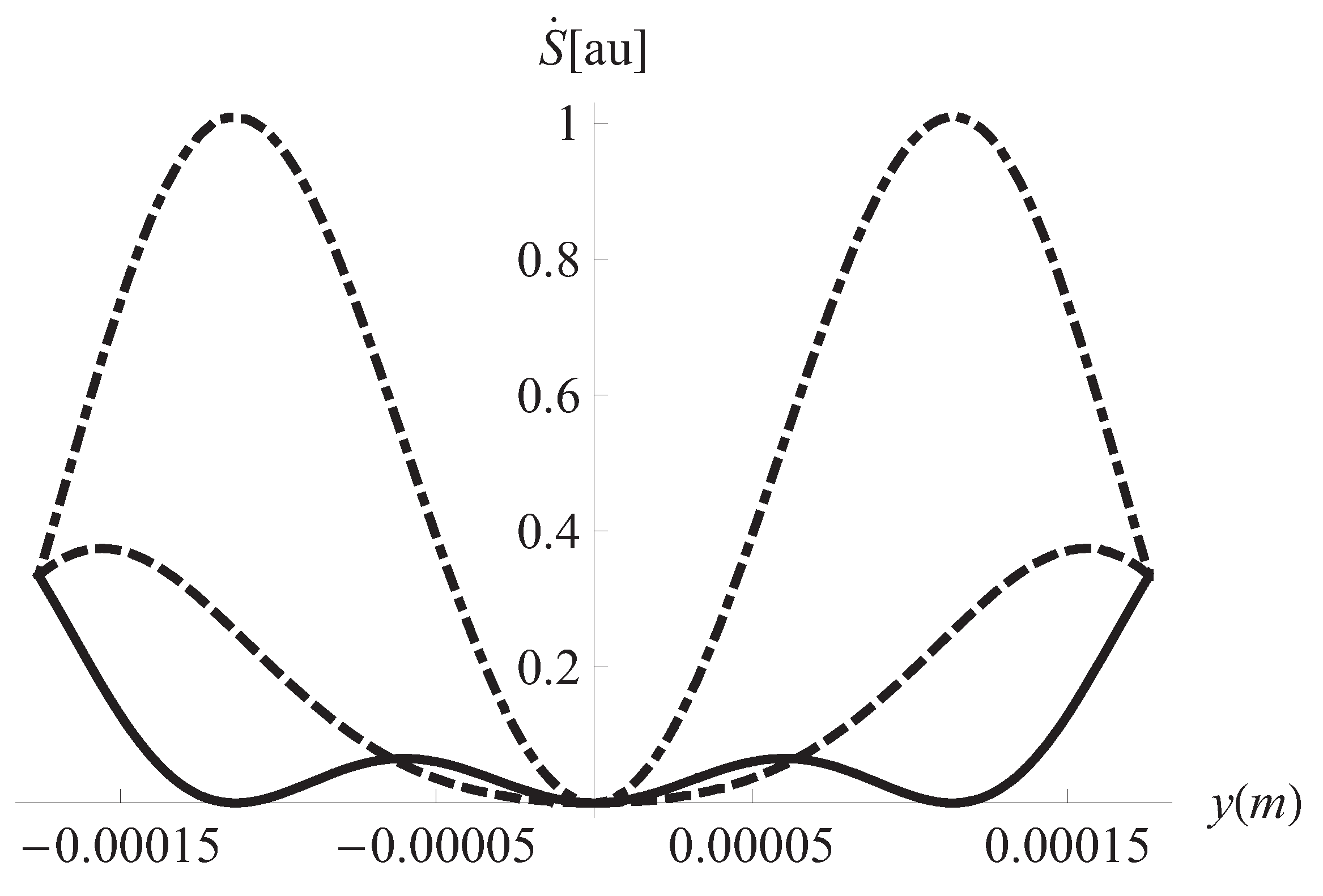


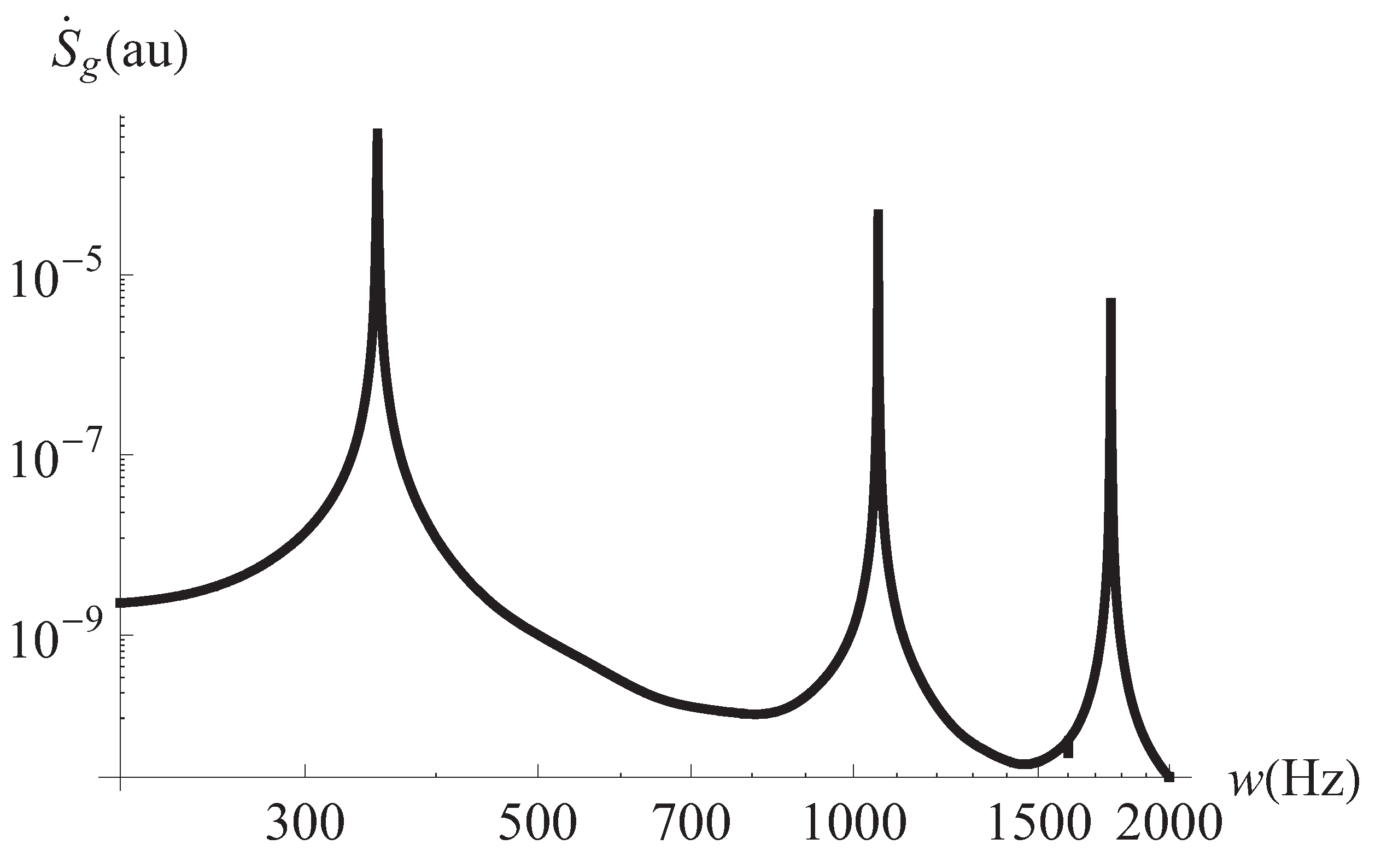
4. Summary and Conclusions
Acknowledgements
References
- Chatwin, P.C. On the longitudinal dispersion of passive contaminant in oscillating flows in tubes. J. Fluid Mech. 1975, 71, 513–527. [Google Scholar] [CrossRef]
- Kurzweg, U.H. Enhanced heat conduction in fluids subjected to sinusoidal oscillations. J. Heat Transfer 1985, 107, 459–462. [Google Scholar]
- Kurzweg, U.H. Enhanced heat conduction in oscillating viscous flows within parallel-plate channels. J. Fluid Mech. 1985, 156, 291–300. [Google Scholar] [CrossRef]
- López de Haro, M.; del Río, J.A.; Whitaker, S. Transport Porous Media 1996, 25, 167.
- del Río, J.A.; López de Haro, M.; Whitaker, S. Enhancement in the dynamic response of a viscoelastic fluid flowing in a tube. Phys. Rev. E 1998, 58, 6323–6327. [Google Scholar] [CrossRef]
- del Río, J.A.; López de Haro, M.; Whitaker, S. Erratum: Enhancement in the dynamic response of a viscoelastic fluid flowing in a tube. Phys. Rev. E 2001, 64, 039901. [Google Scholar] [CrossRef]
- Tsiklauri, D.; Beresnev, I. Enhancement in the dynamic response of a viscoelastic fluid flowing through a longitudinally vibrating tube. Phys. Rev. E 2001, 63, 046304–046308. [Google Scholar] [CrossRef]
- Castrejón-Pita, J.R.; del Río, J.A.; Castrejón-Pita, A.A.; Huelsz, G. Experimental observation of dramatic differences in the dynamic response of Newtonian and Maxwellian fluids. Phys. Rev. E 2003, 68, 046301–046305. [Google Scholar] [CrossRef]
- Lambert, A.A.; Ibáñez, G.; Cuevas, S.; del Río, J.A. Optimal behavior of viscoelastic flow at resonant frequencies. Phys. Rev. E 2004, 70, 056302. [Google Scholar] [CrossRef]
- Lambert, A.A.; Ibáñez, G.; Cuevas, S.; del Río, J.A. Erratum: Optimal behavior of viscoelastic flow at resonant frequencies. Phys. Rev. E 2006, 73, 049902. [Google Scholar]
- Yakhot, V.; Colosqui, C. Stokes’ second flow problem in a high-frequency limit: Application to nanomechanical resonators. J. Fluid Mech. 2007, 586, 249–258. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation through Heat and Fluid Flow; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Bejan, A. Minimization of Entropy Generation; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Sobhan, Ch.B.; Garimella, S.V. A comparative analysis of studies on heat transfer and fluid flow in microchannels. Microscale Thermophys. Eng. 2001, 5, 293–311. [Google Scholar] [CrossRef]
- Guo, Z.-Y.; Li, Z.X. Size effects on microscale single-phase flow and heat transfer. Int. J. Heat Mass Tran. 2003, 46, 149–159. [Google Scholar] [CrossRef]
- Guo, Z.-Y.; Li, Z.X. Size effects on single-phase channel flow and heat transfer at microscale. Int. J. Heat Fluid Flow 2003, 24, 284–298. [Google Scholar] [CrossRef]
- Morini, J.L. Single-phase convective heat transfer in microchannels: A review of experimental results. Int. J. Therm. Sci. 2004, 43, 631–651. [Google Scholar] [CrossRef]
- Bayraktar, T.; Pidugu, S.B. Characterization of liquid flows in microfluidic systems. Int. J. Heat Mass Tran. 2006, 49, 815–824. [Google Scholar] [CrossRef]
- Hooman, K. Entropy generation for microscale forced convection: Effects of different thermal boundary conditions, velocity slip, temperature. Int. Comm. Heat Mass Tran. 2007, 34, 945–957. [Google Scholar] [CrossRef]
- Liang, X. Some effects of interface on fluid flow and heat transfer on micro- and nanoscale, jump, viscous dissipation, and duct geometry. Chin. Sci. Bull. 2007, 52, 2457–2472. [Google Scholar] [CrossRef]
- Yao, J.; Yao, Y.F.; Patel, M.K.; Mason, P.J. On Reynolds number and scaling effects in microchannel flows. Eur. Phys. J. Appl. Phys. 2007, 37, 229–235. [Google Scholar] [CrossRef]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Dover: New York, NY, USA, 1984. [Google Scholar]
- Fischer, P.; Rehage, H. Non-linear flow properties of viscoelastic surfactant solutions. Rheol. Acta 1997, 36, 13–27. [Google Scholar] [CrossRef]
- Aydin, O.; Avci, M. Analysis of laminar heat transfer in micro-Poiseuille flow. Int. J. Therm. Sci. 2007, 46, 30–37. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. Simulation of heat and momentum transfer in complex micro-geometries. J. Thermophys. Heat Tran. 1994, 8, 355–370. [Google Scholar] [CrossRef]
- Reichl, L. A Modern Course in Statistical Physics; John Wiley & Sons, Inc.: New York, NY, USA, 1998; Chapter 11. [Google Scholar]
- Oelschlaeger, C.; Schopferer, M.; Scheffold, F.; Willenbacher, N. Linear-to-branched micelles transition: A rheometry and diffusing wave spectrometry (DWS) study. Langmuir 2009, 25, 716–723. [Google Scholar] [CrossRef] [PubMed]
- Rehage, H.; Hoffman, R.H. Rheological properties of viscoelastic surfactant systems. J. Phys. Chem. 1988, 92, 4712–4719. [Google Scholar] [CrossRef]
- Ibáñez, G.; Cuevas, S.; López de Haro, M. Minimization of entropy generation by asymmetric convective cooling. Int. J. Heat Mass Tran. 2003, 46, 1321–1328. [Google Scholar] [CrossRef]
- Ibáñez, G.; Cuevas, S.; López de Haro, M. Thermodynamic optimization of radial MHD flow between parallel circular disks. J. Non-Equilib. Thermodyn. 2004, 29, 107–122. [Google Scholar]
- Vázquez, F.; Olivares-Robles, M.A.; Cuevas, S. Viscoelastic effects on the entropy production in oscillatory flow between parallel plates with convective cooling. Entropy 2009, 11, 4–26. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vazquez, F.; Olivares-Robles, M.A.; Medina, S. Size Effects on the Entropy Production in Oscillatory Flow between Parallel Plates. Entropy 2011, 13, 542-553. https://doi.org/10.3390/e13020542
Vazquez F, Olivares-Robles MA, Medina S. Size Effects on the Entropy Production in Oscillatory Flow between Parallel Plates. Entropy. 2011; 13(2):542-553. https://doi.org/10.3390/e13020542
Chicago/Turabian StyleVazquez, Federico, Miguel Angel Olivares-Robles, and Sac Medina. 2011. "Size Effects on the Entropy Production in Oscillatory Flow between Parallel Plates" Entropy 13, no. 2: 542-553. https://doi.org/10.3390/e13020542